Prepoznavanje štirikotnikov

Ura sodi v matematiko: v njej ponavljamo prepoznavanje različnih vrst štirikotnikov in njihovih lastnosti.

Z vidika umetne inteligence se ukvarjamo z zbiranjem podatkov in njihovo predstavitvijo s tabelo. Spoznamo strojno ućenje: postopek sestavljanja klasifikacijskega drevesa in njegovo uporabo - na papir in/ali z računalnikom. Mimogrede vidimo, da je model, ki je narejen iz (delno) napačnih podatkov, tudi sam (navadno) (delno) napačen.

Tule so navodila za izvedbo, objavljeno pa je tudi dodatno gradivo za učitelje.

Možni scenariji

Uro je možno zapeljati na različne načine.

• Učenci lahko ponavljajo lastnosti in imena štirikotnikov, tako da jih prepoznavajo in zapisujejo na kartice. Če to preskočimo, jim lahko razdelimo listke, na katerih so lastnosti že označene.
• Učenci lahko ročno sestavljajo klasifikacijsko drevo, torej “ključ” za prepoznavanje štirikotnikov. To počnejo tako, da razporejajo listke na mizi in s pleskarskim lepilnim trakom rišejo drevo ter v njegova vozlišča postavljajo kriterije za ločevanje.
• Drevo nato uporabijo za prepoznavanje novih štirikotnikov teh oblik.

Če želimo izvesti uro brez računalnika, lahko tu končamo. Ali pa izpustimo neračunalniški del in tu šele začnemo. Najboljše pa je seveda, da ne izpustimo ničesar. :)

• Učenci prek tablic ali računalnikov vnesejo podatke o štirikotnikih. Spletna stran zbere odgovore vse učencev.
• Podatke uvozimo v Orange in preverimo, kakšno drevo sestavi računalnik.
• Preverimo, ali je drevo pravilno, tako da ročno ugotovimo, ali je skladno z znanimi lastnostmi štirikotnikov in tako, da preverimo, ali pravilno razvršča testne štirikotnike.
• S primernimi gradniki v okolju Orange analiziramo napake, ki so jih naredili učenci. Po tem jih lahko popravimo, tako da podatke prenesemo na računalnik, popravimo v Excelu in nato nalagamo v Orange iz lokalne datoteke. Če želimo, lahko vnašanje v računalnik preskočimo in uporabimo kar vnaprej pripravljene pravilne podatke.
• Končno preverimo še, kako računalnik s sestavljenim modelom prepoznava nove štirikotnike.

Preden v prvem delu ročno sestavimo klasifikacijsko drevo, moramo predstaviti, kako so ta drevesa pravzaprav videti. To je najpreprosteje izvesti tako, da pred to učno uro izvedemo uro s klasifikacijo palčkov oz. gusarjev ali Živalsko drevo. Ura Določevalni ključi za skupine živali pa je morda preveč podobna tej aktivnosti; izvedba obeh je smiselna le, če je njun namen predvsem ponavljanje živalskih vrst oz. vrst štirikotnikov.

Učno uro smo večkrat preskusili tudi tako, da učenci podatkov niso vnašali na papir temveč prek tablic na spletno stran, s katere smo nato zajeli podatke v program Orange. Pri tam je vsaka skupina določila lastnosti in obliko 6-7 likov, končni podatki so obsegali 42 likov. Aktivnost v takšni obliki zahteva manj časa, slabost pa je v tem, da učenci ne sestavijo drevesa ročno. Poleg tega se zbrani podatki nikoli niso pokazali dovolj natančni za smiselno drevo. Na koncu smo vedno pokazali še drevo sestavljeno iz popolnoma pravilnih podatkov.

Priprava podatkov - na papir

Prvi del je predvsem ponavljanje geometrijskih pojmov in prepoznavanje vrst štirikotnikov.

1. V uvodu ponovimo različne vrste štirikotnikov (rišemo na tablo, rišejo jih oni…) in se spomnimo na lastnosti, s katerimi so definirani (vzporedni pari stranic, pravi koti…). Like pustimo narisane na tabli, da se bodo učenci manj motili.

2. Učence razdelimo na primerno velike skupine.

   Velikost je odvisna od tega, kako bomo organizirali označevanje lastnosti štirikotnikov (glej spodaj). Vsaka od skupin bo sestavljala svoje drevo, za kar bo potrebovala nekaj prostora, recimo dve skupaj postavljeni šolski mizi.

3. Vsaka skupina dobi:

   
   • komplet kartic s štirikotniki (številke 10-45); če želimo zmanjšati količino dela, jim damo manj likov, poskrbimo pa, da ima vsaka skupina vsaj dva lika vsake vrste;
   • kartice s testnimi primeri (številke 50-57); te prepognemo in jih razdelimo tako, da je lik skrit. Seveda bodo učenci lahko poškilili; bistvo je, da se skupaj z učenci “delamo”, da ne vemo, za katero vrsto štirikotnika gre in o tem sklepamo iz popisanih lastnosti, ne iz slike;
   • listke s kriteriji, razrezanimi na tretjine, kot je označeno.
   • listke z imeni likov.

4. Skupina za vsak štirikotnik označi njegove lastnosti.

   • Prvi krog pobarvajo z rdečo, če so vse stranice enako dolge ali z modro, če ima dva para enako dolgih stranic; sicer ga pustijo nepobarvanega.
   • Drugi krog pobarvajo, če so vsi koti lika pravokotni.
   • Tretjega pobarvajo, z rumeno, če ima dva para enako dolgih stranic in z zeleno, če ima en par enako dolgih stranic.
   • Četrtega pobarvajo, če se diagonali sekata pod pravim kotom.

   Poleg tega morajo za vsak lik napisati ali gre za kvadrat, pravokotnik, romb, paralelogram, deltoid, trapez, ali nič od tega. Zapisati morajo najbolj specifično obliko; vsi rombi so hkrati tudi paralelogrami, trapezi in deltoidi, vendar jih morajo označiti kot rombe.

   Ta naloga je težka, saj zahteva veliko zbranosti. Da bo manj napak, je morda smiselno, da se vsak član skupine specializira za eno lastnost. Eden vzame rdečo barvico in pobarva prvi krog vseh likov z enakimi dolžinami stranic. Drugi z modro barva pobarva prvi krog tistih, ki imajo dva para enako dolgih stranic … in tako naprej. Eden lahko določa obliko likov. Eden lahko skrbi za končno kontrolo pravilnosti. Taka izvedba ima dodatno zanimivo komponento, saj se morajo člani skupine organizirati in si razdeliti delo.

   Vmesna različica je, da dobi vsak svoj kupček in si podajajo barvice, tako da vsak nekaj časa preverja neko lastnost.

   Tu gre očitno za vajo iz matematike, hkrati pa iz organizacije skupinskega dela. Manjše napake ne bodo kritične in jih bodo sami popravili kasneje.

Sestavljanje klasifikacijskega drevesa

V drugem delu sestavimo klasifikacijsko drevo in ga preskusimo.

1. Če smo s temi učenci že prej delali aktivnosti Kaj počnejo palčki ali Živalsko drevo, koncept že poznajo. Sicer jim ga razložimo in z njimi morda opravimo prvi korak: določimo lastnost, po kateri se štirikotniki najbolj razlikujejo. Različne skupine bodo imele morda različna mnenja o tem, katera lastnost bi to bila: s tem ni nič narobe, saj je v resnici vseeno. :)

2. Vsaka skupina naj se odloči za določeno lastnost. Na mizo postavi list s tem kriterijem, na levo in desno (in naravnost, če so možnosti tri) “nariše” črto s pleskarskim lepilnim trakom ter razdeli štirikotnike glede na to lastnosti in jih postavi na konec “narisane” črte. Nato za vsako podskupino štirikotnikov določi novo primerno lastnost in jih razdeli. To ponavljajo, dokler ne dobijo čistih skupin.

3. Delitev na podskupine nadaljujejo, dokler ne dobijo čistih skupin. Če so v prvem koraku razdelili štirikotnike glede na to, ali imajo same prave kote ali ne, bodo na eni strani dobili pravokotnike in kvadrate, na drugi vse ostalo. Ko bodo hoteli razdeliti pravokotnike in kvadrate, bodo morali poiskati lastnost, po kateri se le-ti razlikujejo. Ta, očitno, ne bo “lik ima dva para vzporednih stranic”, saj to velja tako za štirikotnike kot za kvadrate. Če je torej izbira kriterija v prvem koraku načelno poljubna, morajo biti v naslednjih korakih izbori bolj premišljeni.

   

   Že med sestavljanjem drevesa bodo najbrž opazili kakšno napako: morda bodo šli vsi paralelogrami na levo, eden pa na desno. To je očitno narobe: narobe je označena bodisi lastnost bodisi lik. Morda tisti, ki gre desno, v resnici sploh ni paralelogram, temveč gre za romb in je čisto prav, da je šel desno. Morda pa je pomotoma označeno, da so vse stranice enako dolge, čeprav ima lik dva para enako dolgih stranic, kar je razlog, da smo ga poslali desno namesto levo.

   Odkrite napake naj kar sproti popravijo.

4. Nato preverimo, ali so drevesa, ki so jih dobile skupine, smiselna. Za vsak končni kupček likov naj preverijo, ali so vsi liki iste vrste (sami rombi, sami pravokotniki) in ali so lastnosti, ki jim jih s kriteriji na poti pripisuje drevo, res takšne, kot vemo iz matematike.

5. Končno lahko odstranijo kupčke z liki in na njihova mesta prilepijo listke z imeni likov.

6. 

   Zdaj pridejo na vrsto prepognjeni listki. Ti imajo na eni strani zapisane (in že označene!) lastnosti, na drugi strani pa je skrit lik in njegovo ime.

   Z vsakim od teh listkov sledimo poti na drevesu. Začnemo v korenu. Če ta usmerja vse like s samimi pravimi koti desno, ostale levo, preverimo, ali je na listku označeno, da ima lik same kote in ga premaknemo v pravo smer. Če naslednje križišče preverja število parov vzporednih stranic in za naš lik piše, da ima en par, gre naprej po srednji poti. Ko pridemo do konca, v drevesu preberemo, za kakšen lik naj bi šlo. Takrat obrnemo listek in preverimo, ali je res.

   En primer lahko pokažemo frontalno oziroma pri eni skupini. Za ostale testne like učenci to opravijo sami.

Vnašanje podatkov v računalnik

Če želimo, lahko nadaljujemo z vprašanjem, ali bi znal - in kako - takšno drevo sestaviti tudi računalnik. Za to lahko uporabimo že pripravljene pravilne podatke; v tem primeru ta odsek preskočimo. Najbrž pa je zanimiveje, če učenci vnesejo svoje podatke iz prvega dela aktivnosti in se računalnik nauči razbirati oblike likov iz njihovih podatkov.

1. 

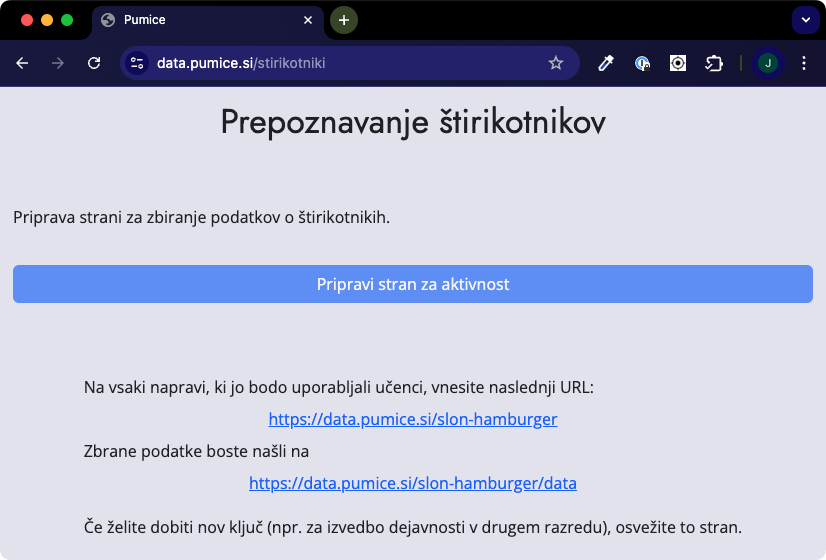
   Na strani https://data.pumice.si/stirikotniki pripravimo stran za vnašanje podatkov. Po pritisku na “Pripravi stran za aktivnost” dobimo povezavo, ki jo vpišemo v naprave (tablice, računalnike), s katerimi bodo učenci vnašali podatke.

   Vse skupine lahko uporabijo isto povezavo, tako da bodo v eni tabeli zbrani rezultati vseh skupin. Če želimo podatke skupin zbirati ločeno, pa osvežimo stran in naredimo novo povezavo za vsako skupino. Tako bomo lahko opazovali napake v drevesih iz podatkov vsake posamične skupine. Nekaj več detajlov najdete v dodatnem gradivu za učitelje.

2. 

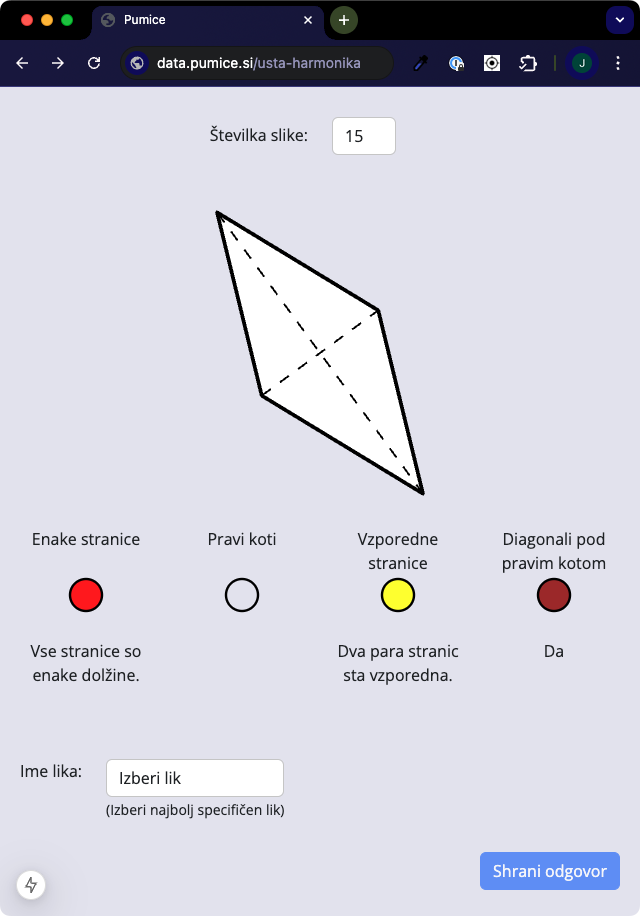
   Učenci na stran vnesejo številke posamičnih likov. S klikanjem na kroge vnašajo njihove lastnosti in na dnu izberejo obliko lika – obrazec ima enako obliko kot kartice, da je prepisovanje lažje. Ko pritisnejo “Shrani odgovor”, nadaljujejo z naslednjim likom.

Sestavljanje in uporaba drevesa

S programom Orange bomo verjetno delali frontalno. Najprej bo računalnik sestavili drevo iz pravilnih podatkov in ga preskusil na novih podatkih: delal bo z enakimi podatki kot učenci in opravil natančno enako delo, kot so ga oni.

Če želimo, lahko namesto že pripravljenih pravilnih podatkov poskusimo delati s podatki, ki so jih zbrali učenci. Kako, je opisano v prvi točki naslednjega odseka. Če se izkaže, da je v njih preveč napak, se vrnemo na pravilne podatke na naslovu https://pumice.si//aktivnosti/stirikotniki/resources/stirikotniki.xlsx .

Tule so navodila po korakih - klikni tu, odpri tisto. Kogar zanima več, naj si poteši radovednost v dodatnem gradivu za učitelje.

1. 

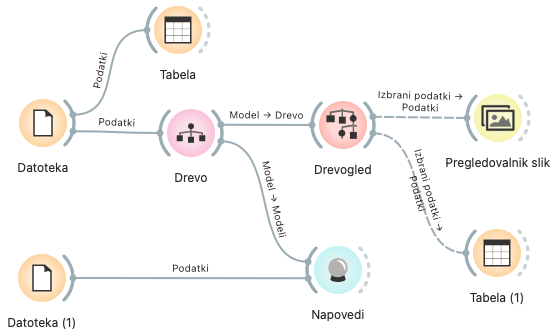
   Prenesemo že pripravljen delotok in ga odpremo v programu Orange. Če nimamo nameščenega dodatka Image Analytics, nas bo Orange na to opozoril, ga po naši potrditvi namestil in se ponovno zagnal.

2. 

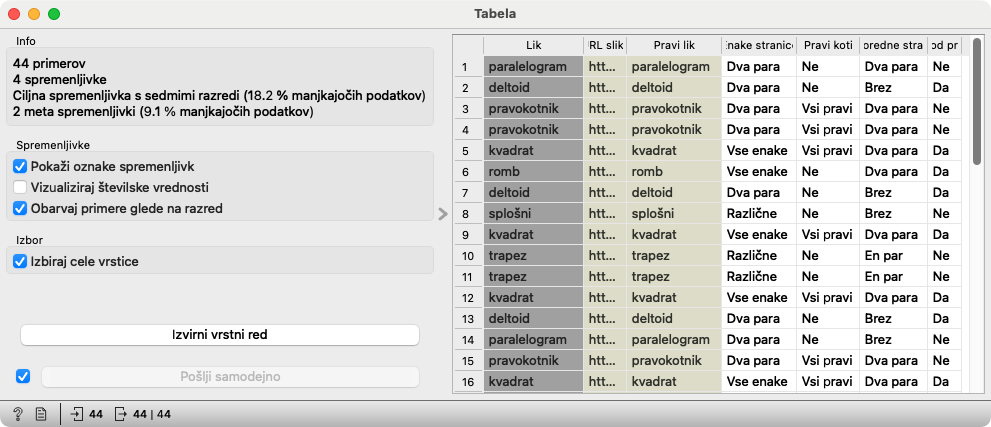
   Z dvoklikom odpremo gradnik Tabela, da učencem pokažemo podatke, ki smo jih naložili. Gre za pravilne podatke, prebrane s te spletne strani. Vsaka vrstica se nanaša na enega od likov in vsebuje njegovo obliko (romb, kvadrat…) ter, po posamičnih stolpcih, njihove lastnosti. (V posebnem stolpcu je še povezava na sliko, ki nam bo prišla prav kasneje.)

3. 

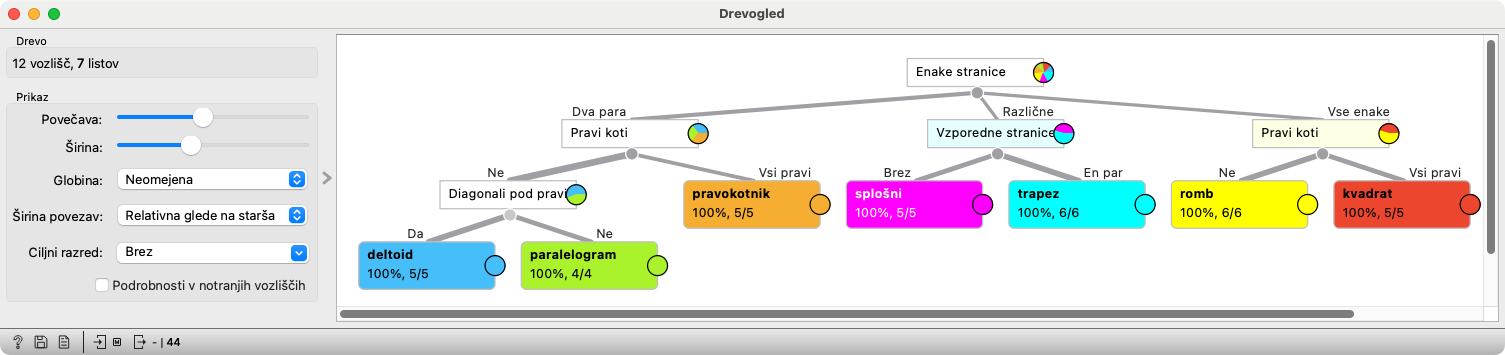
   Odpremo Drevogled. V njem vidimo drevo, sestavljeno iz pravilnih podatkov. Najbrž je drugačno od drevesa, ki so ga sestavili učenci. Je vseeno pravilno?

4. 

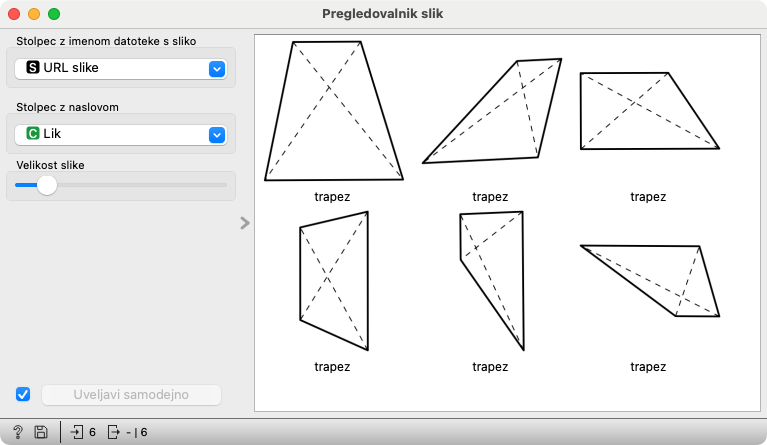
   Odprimo še Pregledovalnik slik. Postavimo Drevogled in Pregledovalnik tako, da bomo videli oba hkrati.

   Zdaj lahko klikamo po posameznih delih drevesa in vidimo like, ki se znajdejo v njem. Tudi takrat, ko so drevo sestavljali učenci, so imeli v posamičnem koraku v različnih delih drevesa kupčke kartic z liki. Računalnik je torej sestavljal drevo natančno tako, kot so ga sestavljali oni.

5. 

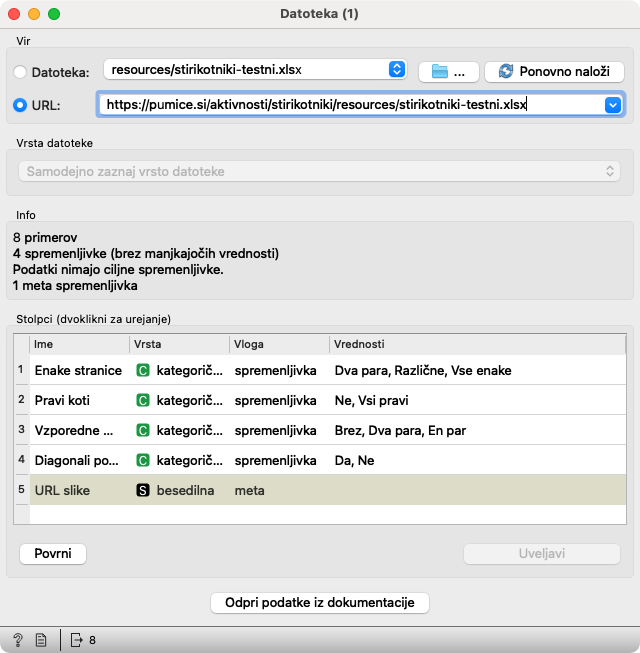
   Drugi gradnik datoteka prebere testne podatke. Ti podatki so enaki likom na prepognjenih karticah.

   Nanj je pripet gradnik Tabela, v katerem lahko učencem pokažemo, da so v njih zgolj opisi lastnosti likov.

6. 

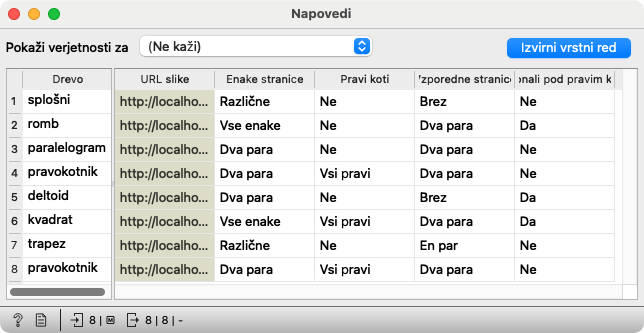
   Gradnik Napovedi dobi podatke iz drugega gradnika Datoteka in model iz gradnika Drevo. V gradniku vidimo, kako je računalnik razvrstil nove like.

7. 

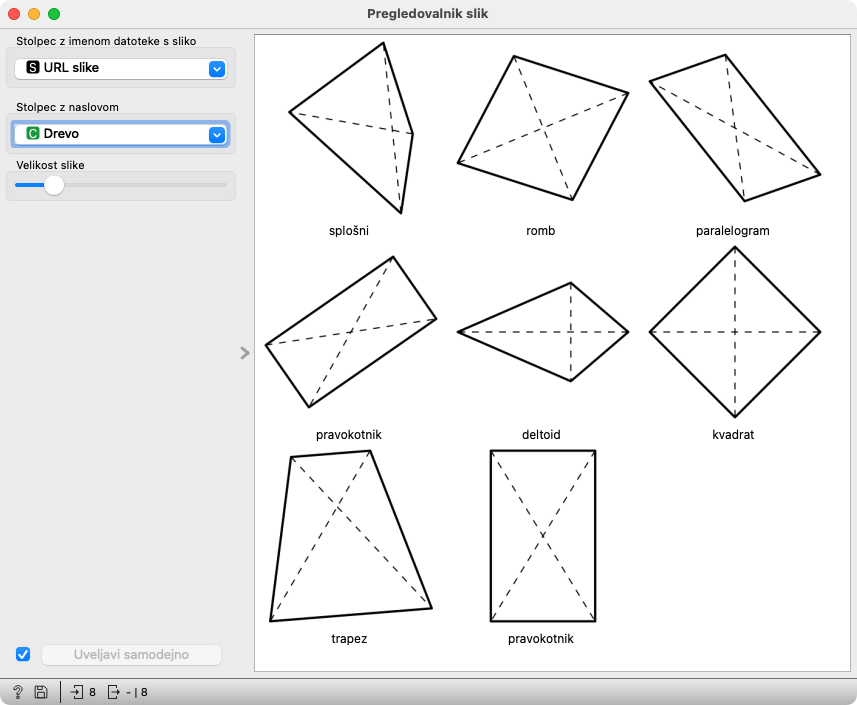
   Je prav? Ni prav? To lahko pogledamo v Pregledovalniku slik, ki je priključen na Napovedi. Pokazal bo slike likov in če kot “Stolpec z naslovom” izberemo Drevo, bomo videli, kako jih prepoznava drevo.

Podatki učencev

Če so učenci vnašali svoje podatke o likih, sestavimo drevo še iz njihovih podatkov. To bo zanimivo zato, ker bo drevo skoraj gotovo (vsaj) nekoliko napačno. Napake bodo posledica napak v podatkih: poiskali jih bomo in tako videli, katere like smo napačno opisali ali uvrstili.

1. 

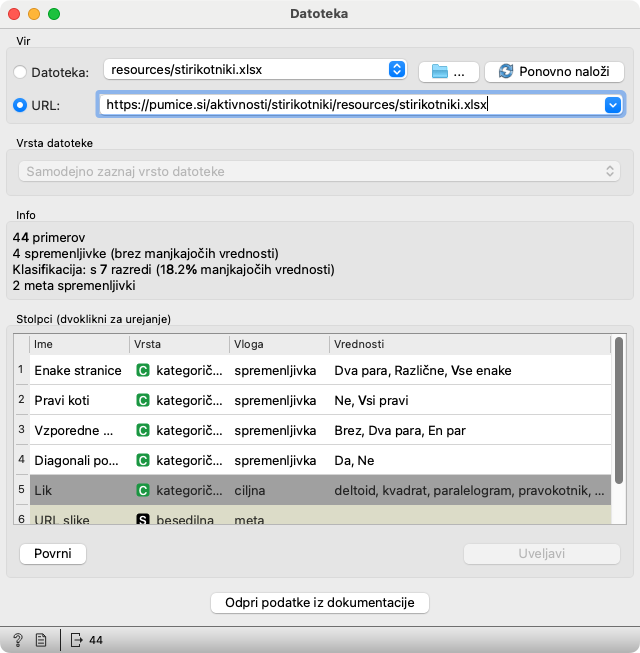
   Odpremo gradnik Datoteka in v polje URL vpišemo povezavo, prek katere so vnašali podatke, le na konec dodamo še /data: če je bila povezava na obrazec https://data.pumice.si/vreme-krogla, so zbrani podatki na https://data.pumice.si/vreme-krogla/data.

2. Spet odpremo Drevogled, v katerem nas že čaka novo drevo. Je pravilno?

   Napake bomo prepoznali po tem, da bo drevo preveliko: namesto, da bi bili vsi liki iste vrste, recimo rombi, v enem samem “listu” drevesa, jih bomo našli na več koncih. Pogledamo, katere lastnosti nas vodijo do posamičnega lista in opazili bomo, da so nekatere napačne. Tako se lahko, recimo, zgodi, da bo do nekega romba vodila lastnost “ima dva para enako dolgih stranic”.

   Še verjetneje se bo zgodilo, da bomo imeli v kakem listu mešanico likov; to vidimo po tem, da tortni diagram, narisan v kotu, ni ene same barve. Če imamo nekje mešanico rombov in deltoidov, ki so si enaki po vseh lastnostih - je to res lahko pravilno?

Iskanje in popravljanje napak

Do napak pride, ker so učenci napačno opisali lastnosti nekaterih likov ali pa so jih napačno poimenovali. Da odkrijemo napake, uporabimo dva gradnika: Pregledovalnik slik in gradnik Tabela, ki je priključen na drevo.

Če želimo popravljati napake in opazovati, kako postaja drevo pravilnejše, torej storimo tako.

1. Prenesemo podatke v Excel: povezavo na podatke, na primer https://data.pumice.si/vreme-krogla/data, vnesemo v brskalnik in dobili bomo datoteko, ki jo odpremo z Excelom.

2. Odpremo gradnik Datoteka, kliknemo tipko z znakom za mapo in tremi pikami, ter izberemo datoteko, ki smo jo pravkar prenesli.

3. Če v Drevogledu kliknemo na “sumljive” liste drevesa, bomo, kot že vemo, v Pregledovalniku slik videli like, ki so uvrščeni vanj. Če vidimo same rombe, vendar pri enem piše “deltoid”, vemo, da gre za napačno poimenovanje. (Drevogled ima polje Stolpec z naslovom. Če izberemo “Lik”, bo kazal imena, ki so jih dodelili učenci, če “Pravi lik” pa prava imena likov.)

   Če pa se je v družbi samih rombov znašel nek deltoid (ki je, sodeč po sliki v resnici deltoid!), je napačna ena od njegovih lastnosti. V gradniku Tabela pa vidimo opise vseh likov v izbranem listu drevesa.

4. V Excelu popravimo odkrito napako in shranimo datoteko.

5. V gradniku datoteka pritisnemo Ponovno naloži, da preberemo popravljene podatke.

6. Pogledamo, ali je drevo pravilno. Če ni, se vrnemo na korak 3.

Diskusija ob koncu

Kdaj lahko za neko napravo rečemo, da je pametna, inteligentna? Je pametni telefon res pameten? Zakaj? Ker nas opozori na rojstne dneve prijateljev - če mu povemo zanje? Je to res “pamet”? Za to je zgolj sprogramiran.

Lahko rečemo, da je računalnik inteligenten, če se nauči nekaj, česar prej ni znal? Tu se je naučil se je razlikovati med štirikotniki - sam, na osnovi primerov. Računalnik ne ve ničesar o rombih in deltoidih, ta imena mu ne pomenijo ničesar. Vse, kar je imel, so bili podatki o likih in iz njih se je uspel naučiti pravila. Točna, če so bili podatki točni in napačna, če so bili v njih napake.

Je torej naredil nekaj za kar ni bil sprogramiran? Da in ne. Ni bil sprogramiran za razlikovanje likov. “Sprogramiral” se je sam. Bil pa je sprogramiran za to, da se uči - da se “samoprogramira”. Je potem pameten ali ne? Ali je potem res pameten ali ne, je stvar pogleda.

Za konec učencem povemo, da se napovedni modeli dandanes uporabljajo vsepovsod. V medicini, na primer, računalniku pokažemo večje število ljudi z različnimi simptomi in mu povemo, katero bolezen imajo; tako se računalnik nauči na podlagi simptomov prepoznavati bolezni, čisto tako, kot se je na podlagi lastnosti štirikotnikov naučil prepoznavati njihove vrste.