Kaj je bilo prej: Fičo ali Jugo?

Učenci v tej uri dobijo kartice s slikami 15 avtomobilov, od zelo starih do najnovejših. Naloga bo razvrstiti avtomobile po starosti. Ko bomo izdali pravi vrstni red, bomo skupaj razmislili, kako številsko oceniti pravilnost njihovih razvrstitev, da bomo lahko ocenili, katera skupina je najboljše opravila nalogo. Nato bomo pogledali, kako uspešno se z nalogo spopade računalnik in opisali, na kakšen način to počne.

Namesto avtomobilov bi lahko uporabili druge slike, ki jih je možno razporediti na časovni trak (izumi, knjige slovenskih pisateljev …) ali poljubne druge objekte, ki jih je možno urejati glede na neko lastnost (slovenski kraji glede na razdaljo od kraja, v katerem stoji šola). Na ta način lahko utrjemo snov pri različnih predmetih.

Pri poskusu v (petem) razredu so avtomobili dekleta pritegnila čisto tako kot fante.

Izvedba zahteva seštevanje in odštevanje števil do 20, na koncu pa seštevanje manjših dvomestnih števil. Razred, v katerem izvedemo uro, je tako odvisen od tega, kako zahtevno snov želimo obravnavati.

Z vidika računalništva in umetne inteligence bomo videli strojno učenje (klasifikacijo) in ocenjevanje kvalitete modelov.

Uro lahko izvedemo tudi brez računalnika. V tem primeru bo z umetno inteligenco povezano le vprašanje, kako ocenjevati pravilnost razvrstitve.

Priprava

Učence bomo razdelili v manjše skupine – po možnosti v pare. Nasvet: če delamo z avti, je boljše, da pari niso mešani, sicer bodo fantje odrinili dekleta, češ da se ta ne spoznajo na avtomobile. Za vsak par bo potrebno natisniti tri liste in dva od njih razrezati.

• 

  S strani https://data.pumice.si/casovni-trak poberemo kartice s slikami. Stran vsebuje slike avtomobilov. Če želimo uporabiti lastne slike, naložimo datoteko xlsx, ki ima v prvem stolpcu zapisane spletne povezave (URL) na slike. Reči naj ne bo preveč, saj jih je potem pretežko urejati; petnajst je kar primerno število.

  Stran bo na vsako sliko dopisala naključno število, iz katerega bo možno izračunati, katera po vrsti je v resnici. Ker želimo pravilo skriti pred učenci, med uro pa jim ga bomo povedali, je stran sestavljena tako, da si vsakič izmisli novo pravilo. Zapišimo si ga!

  

  Za primer kartic z avtomobili, objavljen na tej strani (pripravite si novega, svojega!), dobimo pravo mesto avtomobila tako, da seštejemo drugo in četrto števko ter odštejemo prvo. Avto s številko 2817 je torej na mestu 8+7-2=13.

• Kartice natisnemo in razrežemo. Vsak kupček kartic pomešamo, saj so natisnjene po vrstnem redu.

• Natisnemo še tabelo, ki jo dobimo na tabeli za vpisovanje in izračun rezultatov. Vsaka skupina dobi svojo tabelo.

Urejanje

1. Učence razdelimo v skupine. Vsaka skupina dobi kupček kartic.

2. 

   Vsaka skupina naj uredi kartice po vrsti, od najstarejšega (avtomobila, knjige, izuma) do najnovejšega. O številkah jim rečemo, da so “kar tako”. (Če učenci sprašujejo, ali se bo iz številk nekako razbralo vrstni red, pač priznajmo, saj jim ne bo pomagalo.)

3. 

   Ko skupine končujejo, jim razdelimo liste s tabelami. V drugi stolpec naj prepišejo številke s kartic, v vrstnem redu, po katerem so jih razporedili. To bodo najpreprosteje naredili tako, da en učenec bere številke, drugi pa jih piše.

Preverjanje

1. 

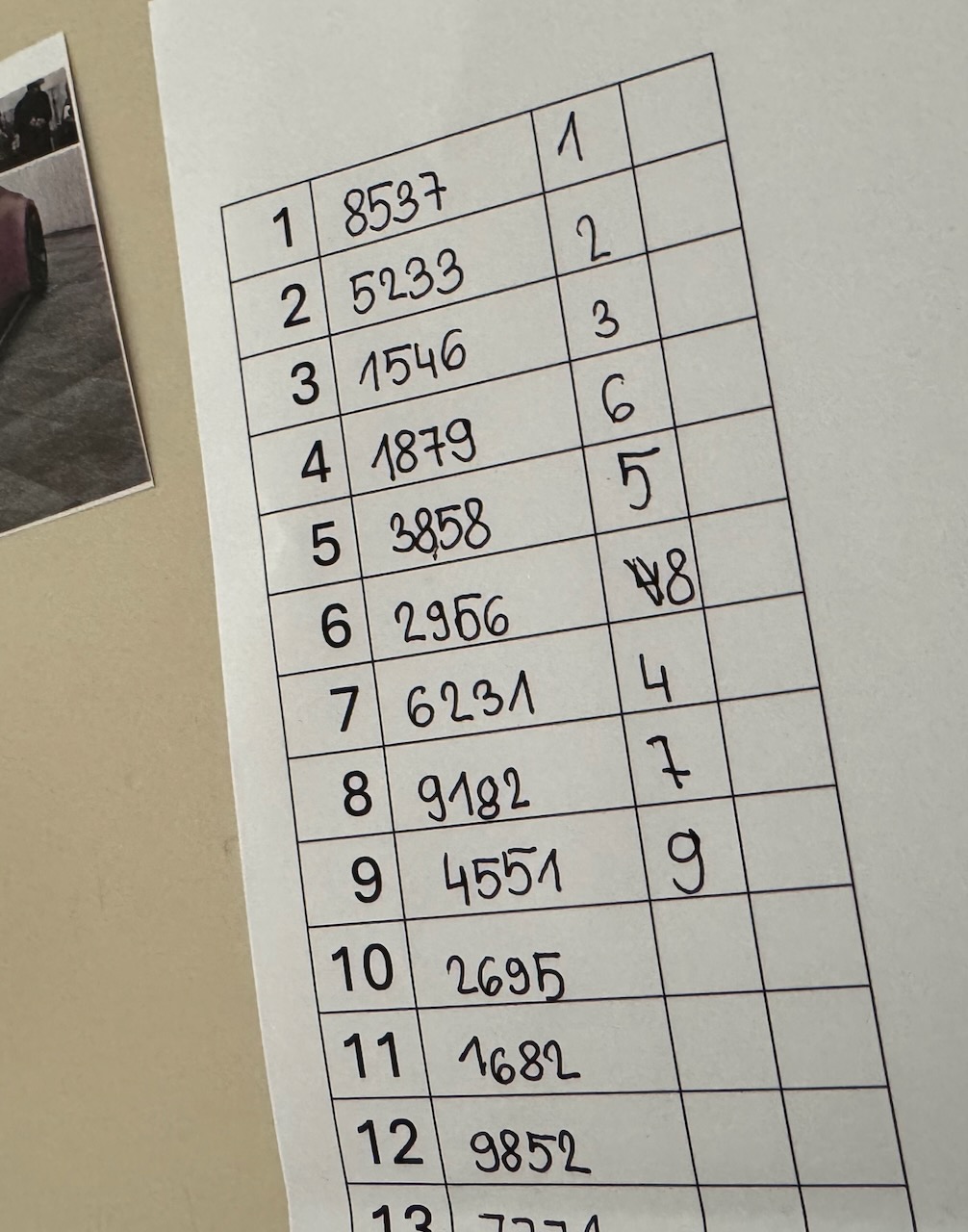
   Učencem povemo pravilo, po katerem lahko iz številk na slikah izračunajo njihovo pravo mesto v razporedu, na primer “seštej drugo in četrto števko ter odštej prvo” (pravilo bo drugačno vsakič, ko pripravimo nov PDF).

   Učenci naj izračunajo pravo mesto vsakega avtomobila in ga zapišejo v tretji stolpec tabele.

2. Kako bi ocenili, katera skupina je najboljše opravila nalogo? Če bodo predlagali kaj v smeri opazovanja vrstnega reda, jih vprašamo, kako bi (številsko) ocenili “napako vrstnega reda”. Vse možnosti so kar zapletene. Ena je, recimo, koliko menjav sosednjih avtov je potrebnih, da preuredimo njihov vrstni red v pravi (Kendallova tau-razdalja). Njen izračun je prezapleten.

   Skoraj gotovo bodo predlagali, da bi prešteli, koliko avtov je na pravem mestu. Tu jim lahko na tablo napišemo takšen protiprimer: na primer, da bi dve skupini dobili takšno tabelo (brez srednjega stolpca):

   Skupina 1			Skupina 2
   1	2		1	8
   2	1		2	5
   3	4		3	2
   4	3		4	4
   5	6		5	6
   6	5		6	3
   7	8		7	1
   8	7		8	7
   .	.		.	.
   .	.		.	.
   .	.		.	.

   Katera skupina je boljša? Leva nima na pravem mestu nobenega avtomobila, desna pa ima na enega, torej je glede na ta kriterij boljša. V resnici pa je leva očitno veliko boljša, le malo smole ima, medtem ko desni … nimajo pojma.

   Prej ko slej bodo prišli na idejo, da bi za vsak avto izračunali, kako daleč je od mesta, od katerega mora biti. Skupna napaka razporeda bi bila enaka vsoti od teh razdalj.

3. 

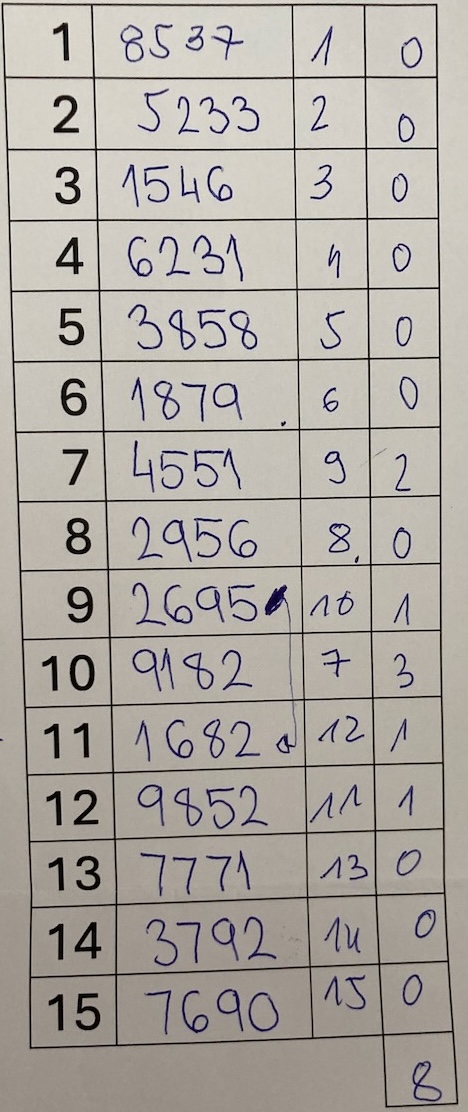
   V tretji stolpec naj zapišejo razdaljo med mestom, ki so ga dali avtomobilu (prvi stolpec) in pravemu mestu. Računajo absolutne razlike. Na tablo napišemo primer in poudarimo, da morajo vedno odštevati manjše število od večjega: če je 12. avto na 8. mestu ali 8. avto na 12. mestu, je razdalja 4.

4. Na koncu naj seštejejo vse razdalje in dobijo skupno napako razporeda. Napišejo ga na dno zadnjega stolpca.

   Zdaj poizvejmo, katera skupina je dosegla najmanjšo napako.

Povezava z umetno inteligenco

Če želimo končati tu, brez računalnika, lahko uro povežemo z ocenjevanjem kvalitete modelov.

Umetna inteligenca temelji na modelih. Model je postopek, po katerem izračuna napoved, odgovor. Veliki jezikovni modeli (large language models, LLM) so modeli, ki na podlagi vprašanja izpišejo odziv. Kot učenci najbrž vedo, so ti modeli različno dobri.

Kvaiteto velikih jezikovnih modelov je težko ocenjevati. Pač pa lahko ocenjujemo preprostejše modele. Model, ki napoveduje, ali bo jutri dež ali sonce, lahko ocenimo glede na to, kolikokrat se zmoti (temu rečemo napovedna točnost). Model, ki mora v zbirki slik poiskati vse slike z mačkami, ocenimo po tem, kakšen delež slik z mačkami je odkril (tej meri rečemo priklic, recall) in koliko od teh slik, ki jih je vrnil, v resnici vsebuje mačko (natančnost, precision).

Ocenjevanje modelov je potrebno zato, da lahko takrat, ko imamo na voljo več modelov, izberemo najboljšega. Ali pa zato, da pri sestavljanju modelov vidimo, ali ga neka sprememba izboljša ali poslabša.

Tudi vsaka skupina učencev je bila neke vrste model in njihovo uspešnost smo primerjali z mero napake, ki smo se je domislili. Zdaj vemo, kdo v razredu je največji ekspert za stare in nove avtomobile.

Mimogrede lahko omenimo še steganografijo, “skritopis”. Steganografija je podobna kriptiranju (“šifriranju”), vendar skriva sporočilo znotraj drugih podatkov. Nekomu lahko, na primer, pošljemo besedilo, ki vsebuje skrivno sporočilo, ki ga dobimo tako da preberemo prve črke vsake vrstice. Tudi kar smo naredili s številkami na karticah z avtomobili, je primer steganografije: pravi vrstni red avtomobilov je bil skrit v številkah na slikah.

Poskus z računalnikom

Opomba: Ta del trenutno deluje le s slikami avtomobilov. Uporaba lastnih slik bi zahtevala boljše poznavanje programa Orange.

1. Učence vprašamo, ali bi znal tudi računalnik razvrstiti avtomobile po starosti.

   Če odgovorijo, da bi “chatGPT” to znal ali da bi računalnik “poiskal te slike na spletu in preveril letnice”: da, vendar nas zanima, ali bi šlo tudi brez tega. Bi se lahko naučil iz slik, ki bi mu jih pokazali prepoznati, kateri avtomobili so starejši in kateri novejši?

2. Naložimo pripravljeni delotok in ga odpremo v programu Orange. Z dvoklikom na Primerjaj pare odpremo gradnik.

3. Razložimo, kako je sestavljen program: program vsebuje “napovedni model”, ki se uči iz primerov. Za vsak par avtomobilov bo napovedal, kateri je starejši, potem pa mu povemo (točneje: program mu po vsaki napovedi sam pove) ali je bila napoved pravilna ali ne.

   Model v začetku ne ve ničesar, zato bo najprej preprosto ugibal, vendar se bo učil iz povratnih informacij o pravilnosti svojih napovedi.

4. 

   Pokažeta se sliki dveh avtomobilov. Ker model ne ve ničesar, ugiba.

5. Pritisnemo Napovej in model naključno izbere enega od avtomobilov kot starejšega, drugega kot novejšega.

   

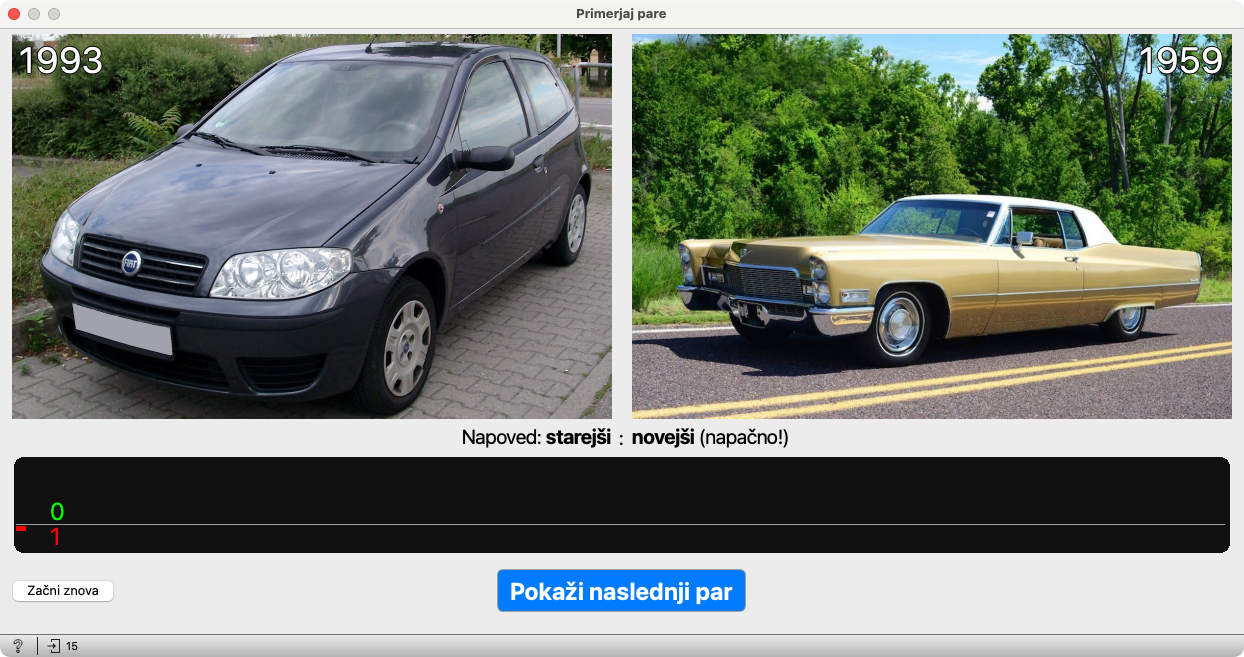
   Nad slikama se pokažeta letnici in pod sliko je napoved modela. V tem primeru je zgrešil. (To se je zgodilo slučajno; lahko bi tudi uganil. Vsekakor pa je boljše, če imamo srečo, da zamenja kak očitno star avto z novim in tako pokaže, da res ne ve ničesar.)

   Poudarimo, da je model po napovedi izvedel, kateri avto je v resnici starejši.

6. 

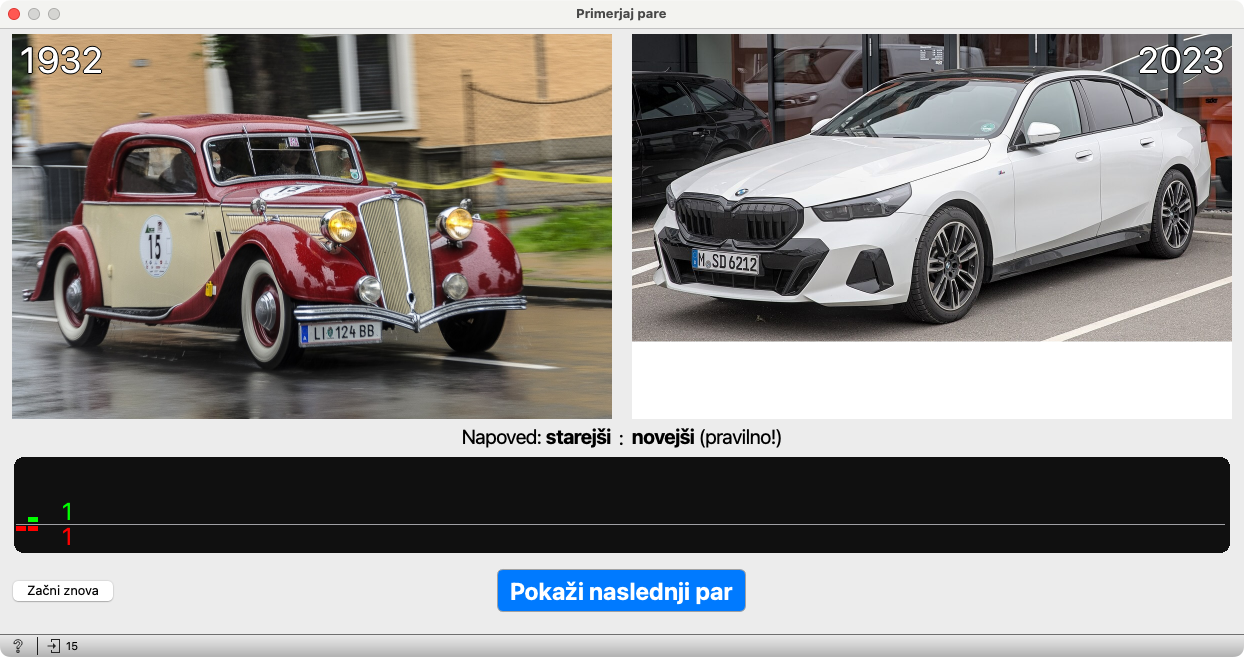
   Nadaljujemo z naslednji parom. Ko pritisnemo Napovej, model ponovno ugiba. Tule je slučajno uganil.

7. Zdaj je model videl že dva para slik in obakrat je izvedel, kateri avtomobil je starejši. Poslej ne bo več ugibal, temveč se bo odločal na podlagi podobnosti z avtomobili, ki jih je videl doslej. Po vsaki napovedi, ki jo naredi, pa še vedno dobi informacijo, ali je bila ta pravilna ali ne.

   

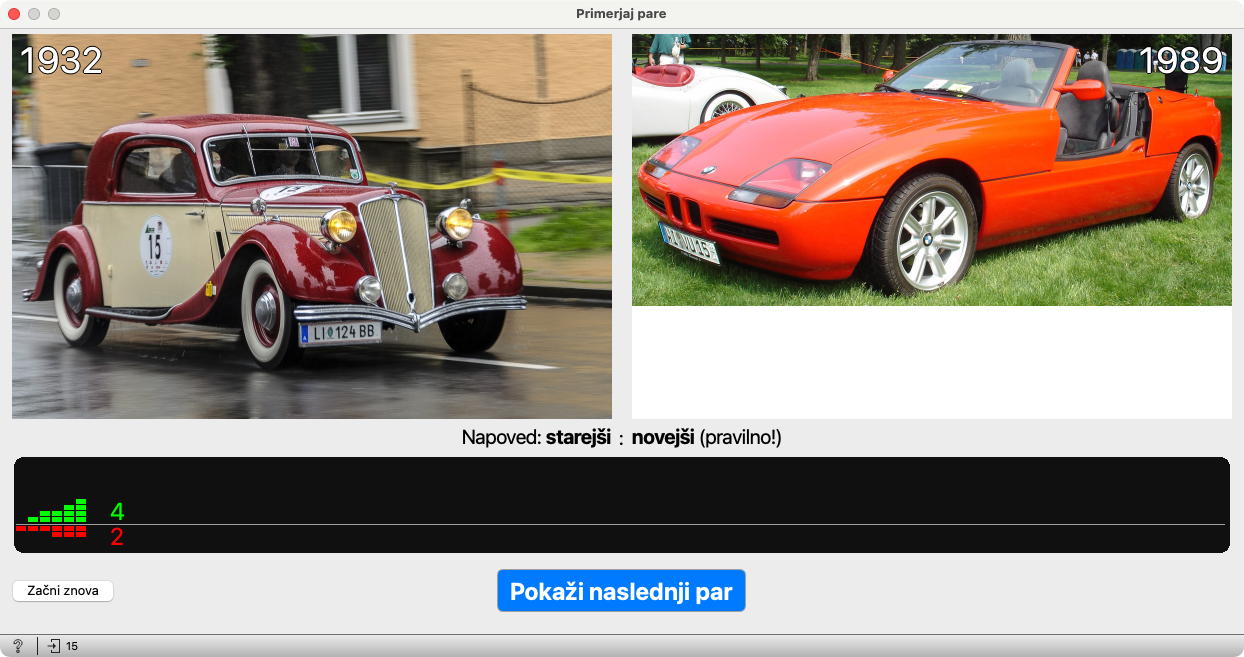
   Nadaljujemo torej s pritiskanjem. Ker se na dnu gradnika izpisuje število pravilnih in napačnih odgovorov, predvsem pa izrisuje graf (vsak stolpec predstavlja nov korak, višina zelenega in rdečega stolpca pa število pravilnih in napačnih odgovorov do tega trenutka), lahko učenci vidijo, kako se računalnik uči. Na začetku dela več napak, kasneje pa te postanejo redke.

   

    

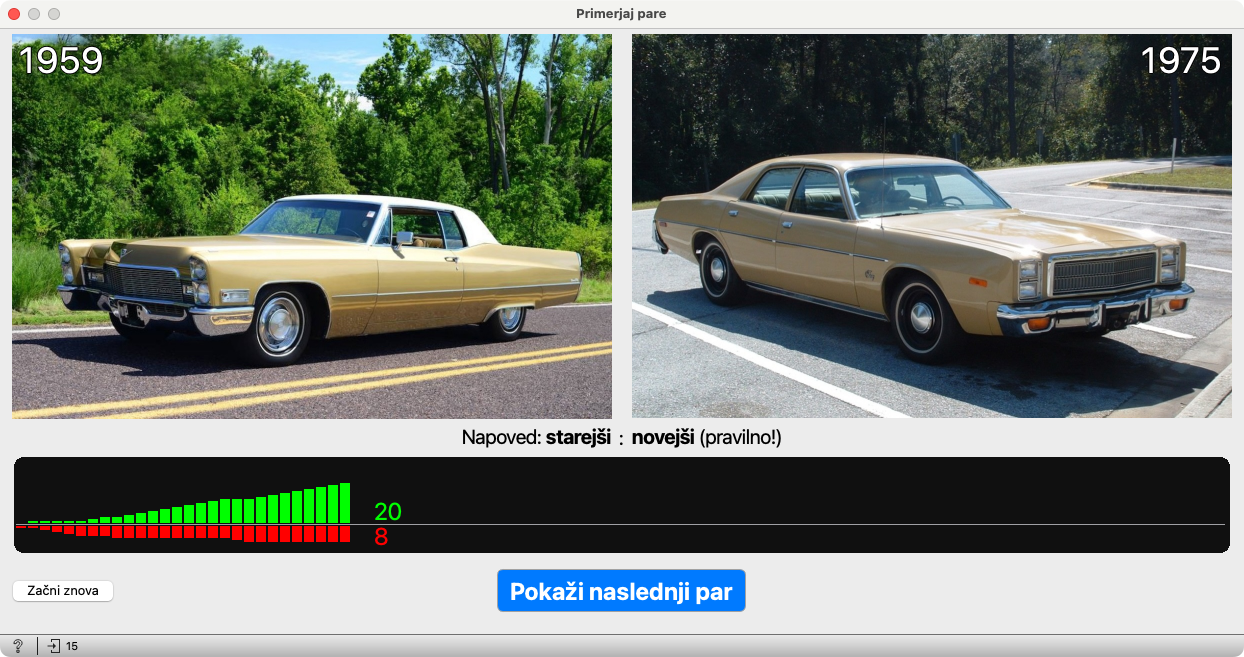
   In bolj in bolj redke …

   

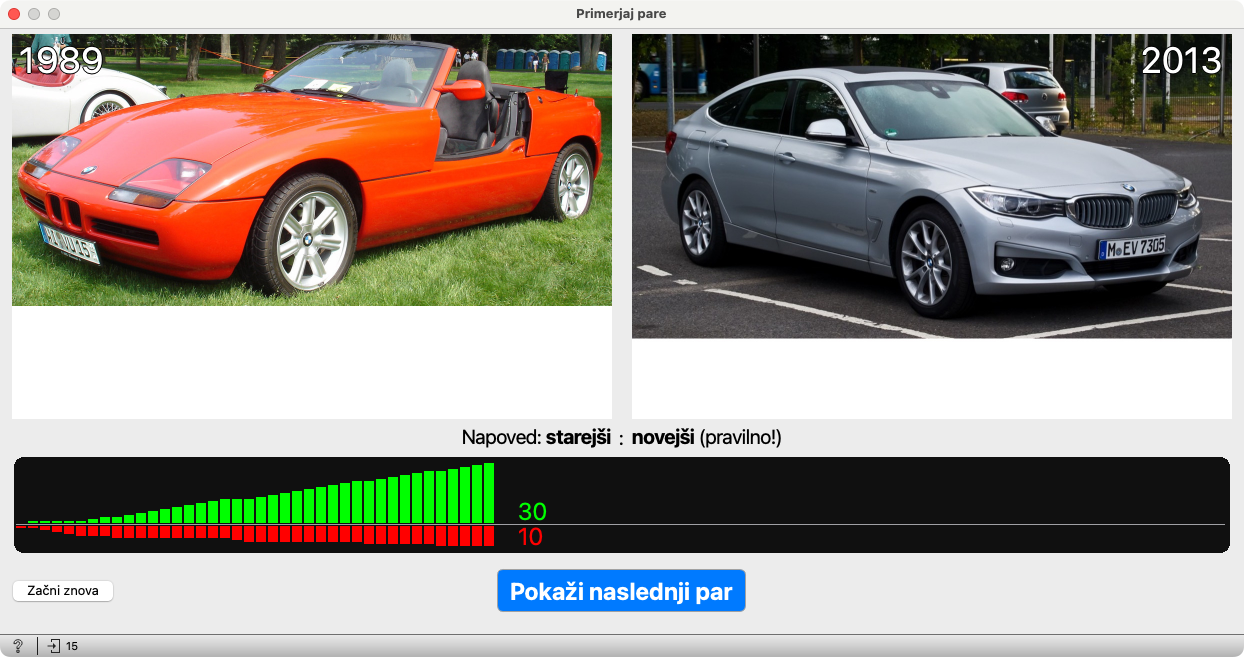
8. Ko postane pritiskanje dolgočasno, lahko uporabimo tipko, s katero naredi računalnik naslednjih pet napovedi, kasneje pa kar tipko, s katero napoveduje, dokler ne zmanjka parov. Tako bomo videli, da se čez nekaj časa praktično ne moti več.

Opcijsko: Razlaga delovanja

Tole bodo izvedli in razložili učitelji, ki se počutijo dovolj suvereni. Spodnji scenarij uporabimo, če se nam zdi smiselno to pokazati z računalnikom. (Je namreč kar impresivno.) Če za to nimamo časa ali znanja, pa lahko razložimo tudi na tablo.

Učence bo zanimalo, kako deluje takšen model. Začnemo s preprostejšim problemom: če bi imel računalnik na voljo številke kartic in če bi mu za nekaj primerov povedali, na katerem mestu v razporedu se nahajajo: bi znal uganiti pravilo, po katerem seštejemo in odštejemo števke, da dobimo pravo mesto?

1. 

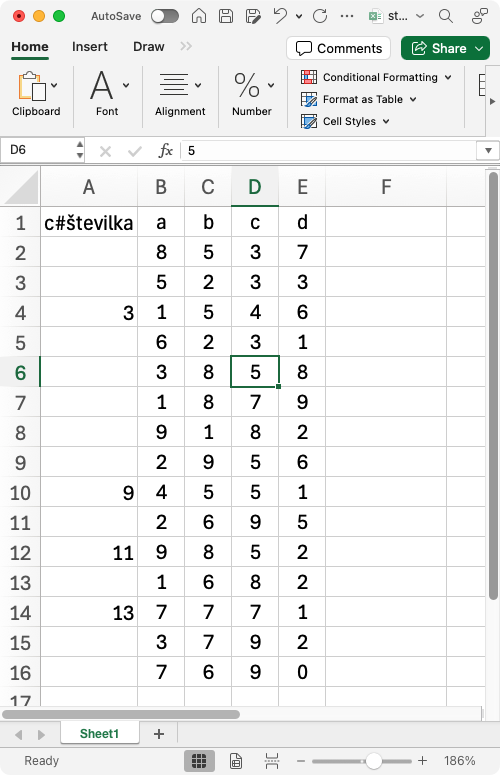
   Poberemo tabelo s številkami in jo za začetek odpremo v Excelu. V stolpcih 2-5 so števke, kakršne bi lahko bile na slikah z avtomobili. Pravilo za te številke je, da seštejemo drugo in tretjo (stolpca označena z “b” in “c”) ter odštejemo četrto (stolpec “d”). Prvi stolpec vsebuje štiri številke, ki jih izračunamo iz števk na desni. Bi lahko računalnik odkril pravilo?

2. 

   Odpremo pripravljeni delotok v Orangu. Gradnik Datoteka prebere gornjo tabelo s spleta. Poda jo gradniku Linearna regresija: njegova naloga je odkriti pravilo, po katerem je treba seštevati in odštevati števke iz štirih stolpcev, da dobimo število v prvem. Gradnik poda sestavljeni model gradniku Napovedi. Slednji poleg tega dobi tudi celotno tabelo s podatki.

3. 

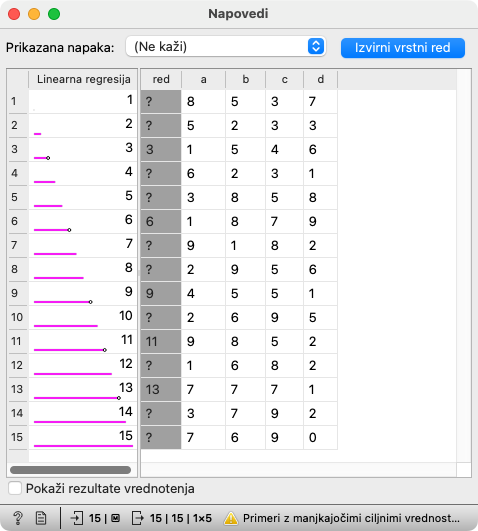
   Odpremo gradnik Napovedi. V skrajnem levem stolpcu (“Linearna regresija”) so izpisane napovedi, ki jih je naredil model: vidimo, da so pravilne: številke od 1 do 15.

   Otrokom povemo, da vrstni red ni pomemben in modelu nič ne pomaga. Da je res tako, lahko dokažemo v naslednjem koraku.

4. 

   Učenci bodo nejeverni, zato storimo naslednje. Gradnik Datoteka trenutno bere podatke s spleta. Namesto tega z njim odpremo isto datoteko, kot jo kažemo v Excelu. Tabelo spremenimo po želji učencev: lahko premešamo vrstice, lahko dodamo nove vrstice (s praznim prvim stolpcem, da vidimo, ali bo znal model napovedati tudi te…). Lahko tudi pobrišemo katero od številk v prvem stolpce (da vidimo, da model po tem ne deluje več) in jo nadomestimo tako, da vpišemo (pravilno) številko v kaki drugi vrstici.

   Po vsaki spremembi moramo shraniti datoteko v Excelu, v Orangu pa v gradniku Datoteka pritisniti gumb “Ponovno naloži”. Nato opazujemo rezultat v gradniku Napovedi.

   Model bo deloval pravilno, če so (pravilno) izpolnjene vsaj štiri vrstice v prvem stolpcu.

5. Učencem povemo, da različnih kombinacij seštevanja in odštevanja pač ni toliko, da jih računalnik ne bi mogel vseh po vrsti preskusiti in odkriti takšne, ki da pravilen rezultat za primere iz prvega stolpca.

   (Lahko jim zamolčmo, da gre za “običajno” linearno regresijo, ki sodi bolj v domeno statistike kot umetne inteligence. Računalnik ne “preskuša različnih kombinacij”, temveč le izračuna koeficiente. Vse to za potek ure ni pomembno.)

6. 

   Zdaj odpremo gradnik Tabela v spodnjem delu delotoka. Ta vsebuje podatke o avtomobilih, s kakršnimi je delal model. Vsaka slika je opisana z 2048 številkami, ki na nek računalniku “razumljiv” način opisujejo njen izgled. Ko je model dobil par slik, je dobil dvakrat po 2048 številk - torej 4096 številk. Tako kot model, ki smo ga kazali v prejšnji korakih, tudi ga model sestavlja vsote, le da sme posamično številko predtem tudi s čim pomnožiti. Tako je lahko, na primer, vzel petkrat prvo številko, od tega odštel sedemkrat drugo in trikrat tretjo.

   Model mora napovedati, kateri avto je starejši, kar naračuna pa je vsota, torej število. Uporabil jo bo takole: če je vsota manjša od nič, je starejši prvi avto, sicer drugi. “Učenje” je zdaj v tem, da mora poiskati tako pravilo za seštevanje teh 4096 števil, da bo vsota dejansko negativna, če je prvi avto starejši, in pozitivna, če je drugi. Iskanje primernega pravila za seštevanje 4096 števil je seveda veliko težje kot iskanje pravila za seštevanje štirih, zato zanj ne zadoščajo le štirje primeri, temveč je model potreboval kakih 20-30 parov, da je poiskal pravilo, ki (dokaj dobro) deluje. Princip pa je isti.