Rezervacije

Uvod

Pogosto obupujemo nad “grozno” sestavljenimi urniki, ki so za nas povsem neustrezni. Le komu je uspelo sestaviti tak urnik? Izkaže pa se, da to sploh ni enostavna naloga. Ukvarjali se bomo z veliko lažjo nalogo urničarja, ki ima na voljo samo eno učilnico in več zahtev za rezervacijo učilnice v različnih časovnih obdobjih. Pravzaprav so zahteve take, da zaradi časovnih konfliktov med njimi vsem ne more ustreči. Nekaj prosilcev bo torej v vsakem primeru razočaranih, urničar pa se trudi, da bo takih čim manj. Kakšno je največje število rezervacij, ki jim lahko ugodi?

Opazovanje podatkov

Podan imamo seznam rezervacij (rezervacije.csv), pri čemer je posamezna rezervacija opisana s časom začetka in konca. Zaradi enostavnosti so ti časi kar v minutah od začetka dneva. Če si na hitro ogledamo podatke, izgledajo takole.

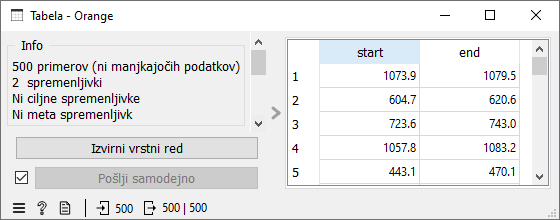
Opravka imamo kar s 500 rezervacijami. Pa so ti podatki kako posebni? Morda se vse rezeracije začenjajo zgodaj zjutraj in raztezajo skoraj čez celoten dan. To bi nam poenostavilo reševanje, vendar že iz prejšnjega ogleda podatkov vidimo, da temu ni tako. Oglejmo si distribucijo začetkov rezervacij. Pri tem nas zanima, v katerem obdobju se nahaja več in v katerem manj začetkov rezervacij.

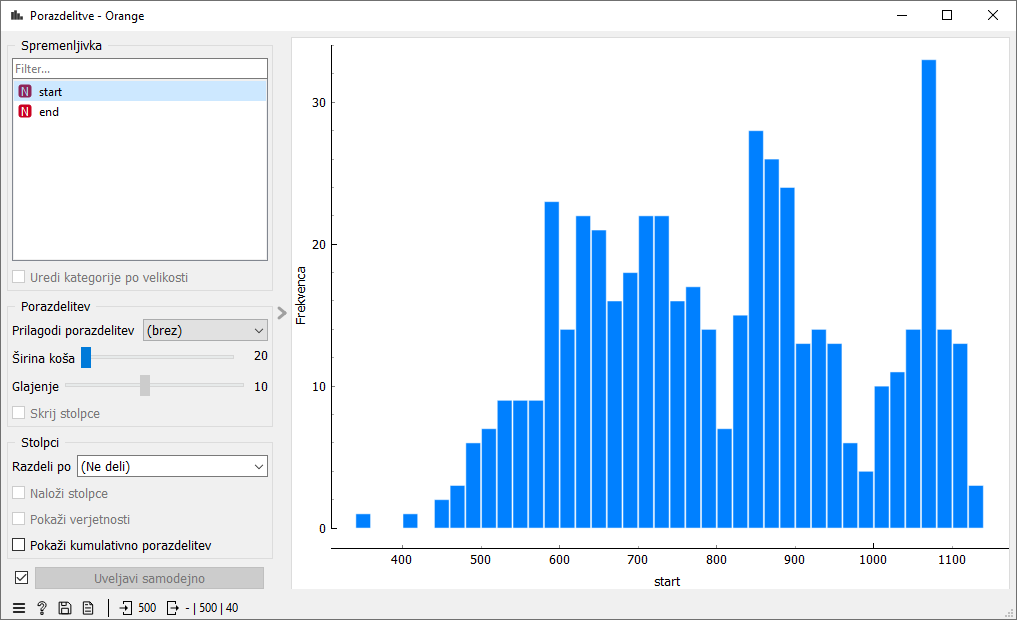
Iz te distribucije pa že lahko razberemo nekaj značilnosti. Obstajajo tri izrazite skupine začetkov rezervacij. Prva skupina je nekje na območju med 500 in 800, druga skupina okoli 900, zadnja pa okoli 1100-te minute. Če to pretvorimo v ure je prva skupina dopoldanska in predstavlja obdobje med 8. in 13. uro. Nato najbrž sledi kosilo. Druga skupina je popoldanska z začetki okoli 15. ure in zadnja večerna okoli 18. ure. Če si ogledamo distribucijo koncev, pridemo do podobnega zaključka.

Konstrukcija novega atributa

Kaj pa dolžine rezervacij? Sta začetek in konec rezervacije povsem neodvisna ali sta kako povezana? V predogledu podatkov lahko hitro opazimo, da sta si začetek in konec precej podobna. Očitno gre (vsaj večinoma) za dokaj kratke rezervacije.

Pogosto v podatkih niso zajeti vsi pomembni atributi. Lahko si pomagamo s kakšno metodo, ki bo poskusila tak atribut sama odkriti. Še raje pa uporabimo svoje znanje s področja rezervacij učilnic in sami dodamo atribut, ki predstavlja dolžino rezervacije, saj nam bo morda prišel prav v nadaljevanju reševanja problema.

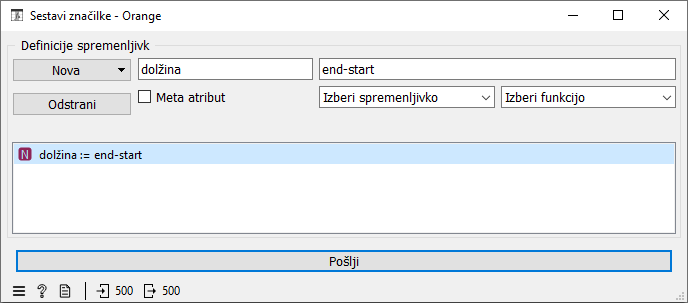
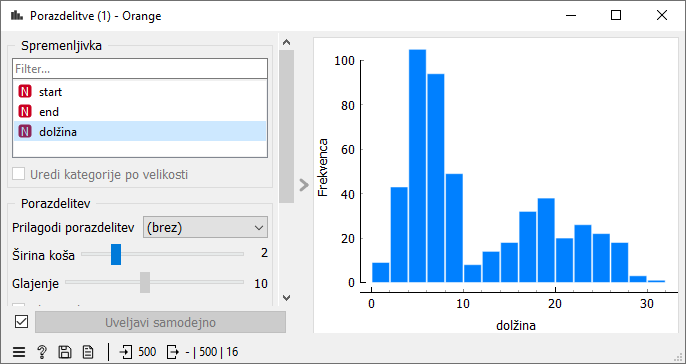
Oglejmo si na hitro še distribucijo dolžine rezervacij. Tudi dolžine niso enakomerno razporejene. Večina rezervacij je kratkih, ki trajajo okoli 5 minut, ostale pa so daljše in zahtevajo nekje med 10 in 30 minut. Glede na količino majhnih rezervacij bo najbrž možno na urnik umestiti kar veliko število rezervacij.

Modeliranje problema

Iz množice rezervacij želimo sestaviti urnik, ki je zaporedje rezervacij, v katerem se vsaka rezervacija začne ob času, ki je večji ali enak koncu predhodne rezervacije v zaporedju.

Probleme bolje razumemo in rešujemo, če jih znamo primerno vizualizirati. Rezervacije lahko predstavimo kot daljice na številski osi, ki predstavlja čas v dnevu. Na spodnji sliki y-koordinata daljic ne igra vloge (na različnih višinah jih narišemo, da je slika pregledna), x-koordinate daljic pa ustrezajo začetkom in koncem rezervacij. Rdeče daljice predstavljajo eno možno zaporedje, ki ustreza urniku. Pravzaprav v tem primeru ni mogoče izbrati več kot 6 daljic, zato je to ena od optimalnih rešitev.

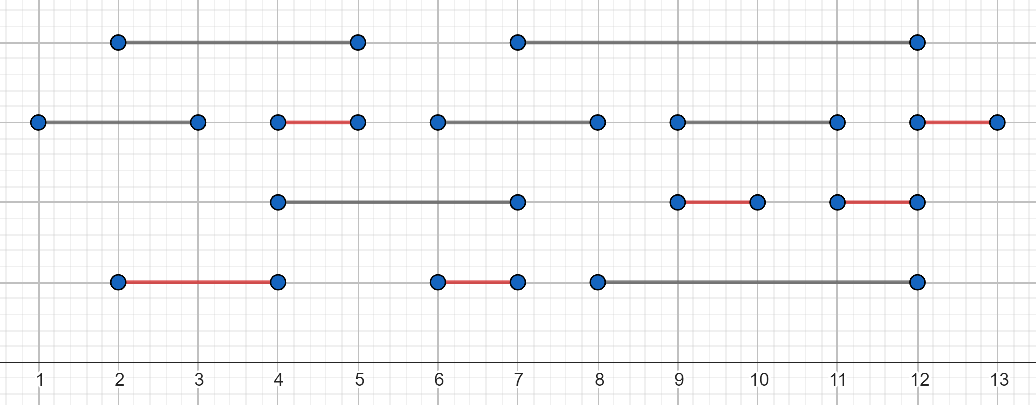
Rezervacije lahko vizualiziramo tudi drugače in sicer kot točke v ravnini. Pri tem naj x-koordinata ustreza začetku rezervacije, y-koordinata pa koncu. Vse točke se bodo torej nahajale nad simetralo prvega kvadranta. Prikažemo jih lahko z razsevnim diagramom. Kako pa izgleda urnik v tej interpretaciji? Če začnemo sestavljati urnik ob času 0, se iz koordinate (0,0) premikamo nekaj časa navzgor, dokler ne pridemo do višine, na kateri se nahaja neka točka. Sedaj se premaknemo desno skozi izbrano točko do simetrale in ponovimo postopek. Tako zgradimo nekakšno stopnišče, cilj pa je sestaviti takega s čim več stopnicami.

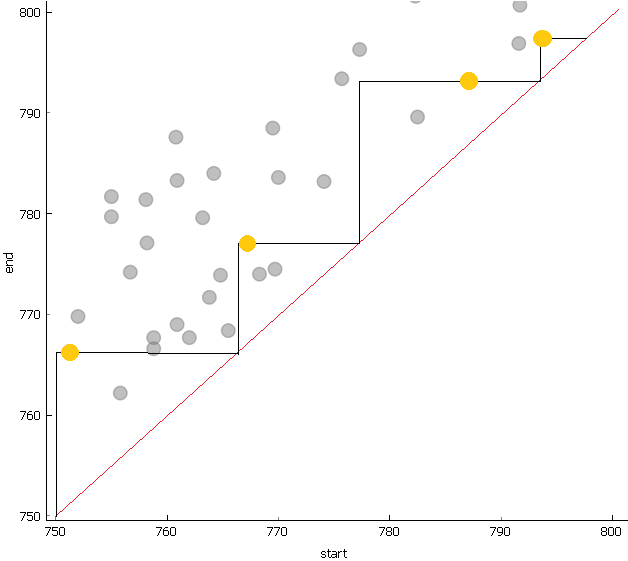
V nadaljevanju se bomo osredotočili na prvo vizualizacijo z daljicami.

Algoritmi

Podano je veliko število rezervacij, zato potrebujemo sistematičen postopek oz. algoritem, s katerim bomo poiskali čim boljši urnik. Oglejmo si tri smiselne ideje in predstavimo še primere implementacij v programskem jeziku Python. Pri tem bomo predpostavili, da imamo rezervacije podane v obliki seznama data, kjer so posamezne rezervacije predstavljene kot slovar s ključema start in end.

data = [{'start': 1073.9, 'end': 1079.5}, {'start': 604.7, 'end': 620.6}, {'start': 723.6, 'end': 743.0} ... ]

1. Ne izgubljajmo časa s čakanjem na naslednjo rezervacijo, zato uvrstimo na urnik rezervacijo z najbolj zgodnjim začetkom. Odstranimo rezervacije, ki imajo konflikt z izbrano, in ponovimo postopek. Spodnja rešitev najprej uredi rezervacijo po njihovem času začetka in vzdržuje čas zaključka zadnje aktivnosti na urniku (time) in število rezervacij na urniku (num). Namesto brisanja rezervacij jih enostavno preskoči.

   data.sort(key=lambda item: item['start'])
   time, num = 0, 0
   for item in data:
       if item['start'] >= time:
           num += 1
           time = item['end']
   print(num)
   

   S strategijo uporabe rezervacij z najbolj zgodnjim začetkom lahko sestavimo urnik z 58 rezervacijami. Hitro pa si lahko izmislimo primer, kjer ta strategija odpove. Če je najbolj zgodnja rezervacija tudi zelo dolga, morda ni najboljša izbira, kar ilustrira spodnji primer.

   

2. Morda bi bilo bolj smiselno najprej izbirati kratke aktivnosti, da se izognemo prejšnji težavi in pri tem povzročamo čim manj konfliktov. Rezervacije uredimo po dolžini od krajših proti daljšim in jih obravnavamo v tem vrstnem redu. Za vsako rezervacijo preverimo, ali jo lahko dodamo na urnik (used). V ta namen moramo preveriti, da se ne seka s katero od aktivnosti na urniku. Če se ne, jo dodamo, sicer pa preskočimo.

   data.sort(key=lambda item: item['end']-item['start'])
   used = []
   for item in data:
       conflict = False
       for other in used:
           if max(item['start'], other['start']) < min(item['end'], other['end']):
               conflict = True
       if not conflict:
           used.append(item)
   print(len(used))
   

   S strategijo izbiranja najkrajših aktivnosti lahko na urnik uvrstimo kar 88 rezervacij. To je občutna izboljšava, ampak še vedno ni optimalna. Si lahko izmislite primer, kjer ta strategija odpove? Tudi kratka rezervacija se lahko seka z več drugimi, zato so lahko boljša izbira daljše rezervacije.

   

3. Izberimo rezervacijo z najbolj zgodnjim koncem, ki nas najmanj omejuje pri izbiri sledečih rezervacij, ker se zgodaj konča. V primerjavi s prvo rešitvijo je razlika samo v vrstnem redu obravnave rezervacij. Tokrat so prej na vrsti tiste z zgodnjim koncem.

   data.sort(key=lambda item: item['end'])
   time, num = 0, 0
   for item in data:
       if item['start'] >= time:
           num += 1
           time = item['end']
   print(num)
   

   S tem postopkom sestavimo urnik z 91 rezervacijami, kar je tudi optimalna rešitev. Da postopek res najde optimalno rešitev, lahko dokažemo s protislovjem. Recimo, da naš urnik (ilustriran v prvi vrsti na sliki spodaj) ni optimalen, torej se z optimalnim (druga vrsta) strinja samo v prvih nekaj rezervacijah (črne barve), nato pa se urnika razlikujeta. V optimalnem urniku lahko zamenjamo to prvo drugačno rezervacijo z našim predlogom, ki ne pokvari preostanka optimalnega urnika, saj se konča najbolj zgodaj (zaradi načina izbire rezervacije v našem algoritmu). Torej obstaja optimalen urnik (tretja vrsta), ki se strinja z našim in je bila predpostavka o obstoju drugačnega optimalnega urnika napačna.

   

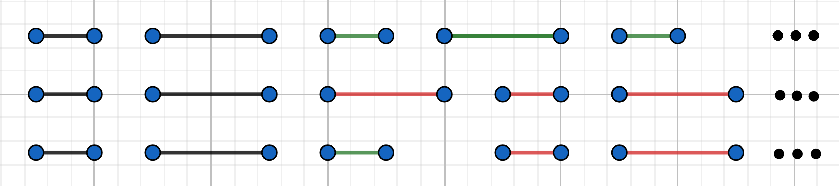
Zaključek

Vizualizacija podatkov je pomemben korak pri reševanju vsakega problema. Omogoča nam boljše razumevanje problema, odkrijemo lahko kakšne posebnosti v podatkih in lažje načrtujemo algoritme za rešitev problema.

Ogledali smo si tri primere požrešnih algoritmov. Požrešni algoritmi (angl. greedy algorithms) so tisti, ki pri gradnji rešitve vedno izberejo potezo, ki v danem trenutku izgleda najbolj obetavno. Kar pa še ne pomeni, da bo to tudi na koncu vodilo do optimalne rešitve. Dve požrešni strategiji nista bili optimalni, tretja pa je bila. Tudi suboptimalni rešitvi sta bili kar uspešni.

Gre za znan problem v računalništvu, ki se imenuje activity selection. Na sorodnem področju razvrščanja (angl. scheduling) se najde še cel kup podobnih zanimivih izzivov.