Nihanje

Aktivnost je namenjena dijakom in dijakinjam višjih letnikov, ki se ne ustrašijo linearnih kombinacij, korenov, eksponentnih funkcij in logaritmov. Poleg tega pa jih zanima “ugibanje” fizikalnih zakonitosti iz podatkov brez fizikalnega predznanja.

Vzmetno nihalo

Ukvarjali se bomo z vodoravnim vzmetnim nihalom. Podan imamo predmet oz. utež z maso m, ki leži na vozičku ali na gladki podlagi brez trenja. Utež je pripeta na steno z vijačno vzmetjo s koeficientom vzmeti k. Utež povlečemo iz ravnovesne lege za odmik d in ga spustimo. Kakšen bo nihajni čas predmeta?

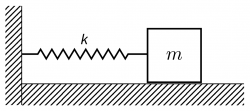
Za začetek malo razmislimo o problemu. Kako masa uteži, koeficient vzmeti in začetni odmik iz ravnovesne lege vplivajo na nihajni čas vzmetnega nihala? Ga povečajo, zmanjšajo ali nanj nimajo vpliva? (Pravilne odgovore bomo odkrili skupaj, ali pa si jih lahko preberete v zaključku).

• Kaj se bo zgodilo z nihajnim časom, če uporabimo utež z večjo maso?
• Kaj pa, če namesto uteži zamenjamo vzmet s tršo, ki ima večji koeficient?
• Bo nihajni čas večji, če predmet potegnemo dlje iz ravnovesne lege?

Spodobilo bi se, da fizikalni pojav opišemo z obstoječim znanjem fizike in tako izpeljemo enačbo za nihajni čas. Mi pa se bomo problema lotili drugače. Iz eksperimentov bomo poskusili določiti enačbo, ki se bo čim bolje ujemala z izmerjenimi podatki in na koncu preverili, kako uspešni smo bili pri tem.

Podatki

Pripravili smo dve podatkovni množici. V prvi je uporabljena samo ena vzmet, v drugi pa različne vzmeti. Obe bi lahko dobili z opravljanjem eksperimentov, vendar smo za potrebe te naloge podatke raje naključno generirali po vnaprej znanih fizikalnih zakonitostih, ki smo jim dodali še malo naključne “merske” napake. Posamezne meritve so opisane z maso uteži m [kg], koeficientom uteži k [N/m], odmikom d [m] in nihajnim časom t [s].

Ena vzmet

Najprej se lotimo lažjega problema, kjer imamo ves čas enako vzmet s koeficientom k = 20 N/m. V razsevnem diagramu si lahko ogledamo odvisnosti atributov, ki nam bodo pomagale pri nadaljnjem modeliranju. Odmik nam ne pove kaj dosti o nihajnem času (spodnja slika, leva stran), zato pa nam precej več pove masa (spodnja slika, desna stran). Večja kot je masa, večji je nihajni čas. Vendar ta odvisnost ni povsem linearna, da bi dvakrat večja masa pomenila dvakrat večji nihajni čas.

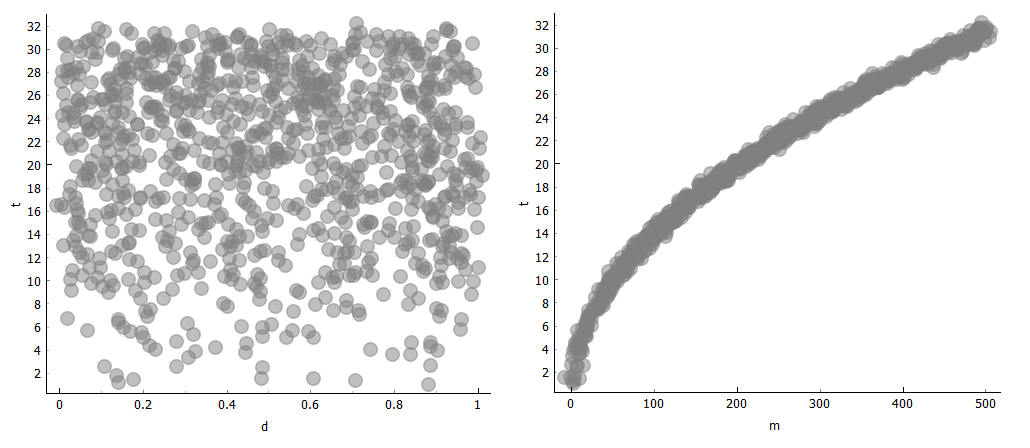
Relacijo med maso in nihajnim časom bomo poskusili čim bolje modelirati z enačbo premice oziroma linearno enačbo t = a₁ + a₂ * m. Želimo poiskati števili a₁ in a₂, da se bo premica čim bolj prilegala podatkom. Uporabili bomo gradnik Polynomial Regression iz dodatka Orange Educational. Ta omogoča iskanje približkov tudi s polinomi višje stopnje, vendar nas bo zanimal približek z linearno funkcijo, ki je polinom prve stopnje.

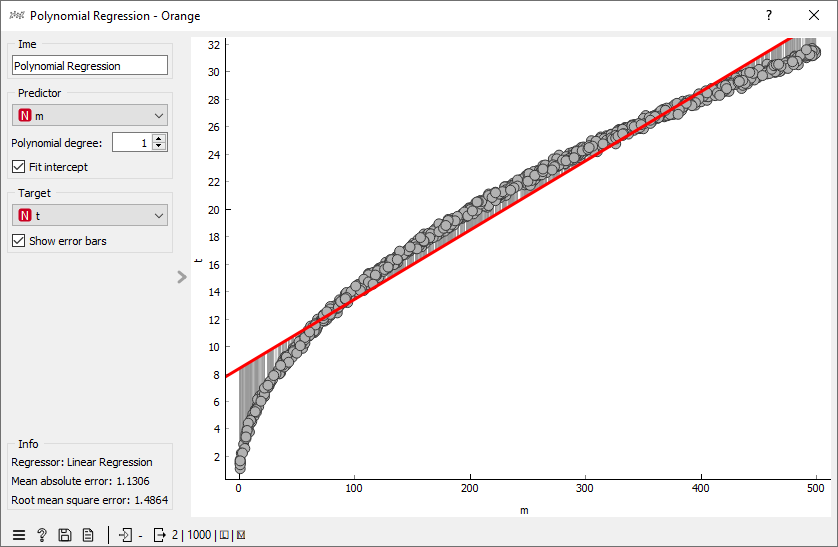
Na sliki vidimo najboljši približek z rdečo črto, z navpičnimi črtami pa so označena tudi odstopanja točk od premice. Ena od mer odstopanja je RMSE (Root mean square error - koren povprečnega kvadrata napake), ki ima v našem primeru vrednost 1,49. Z uporabo tabele si lahko ogledamo tudi dejanske koeficiente premice (v našem primeru je a₁ = 8,39 in a₂ = 0,05). Enačba premice je torej enaka t = 8,39 + 0,05 * m.

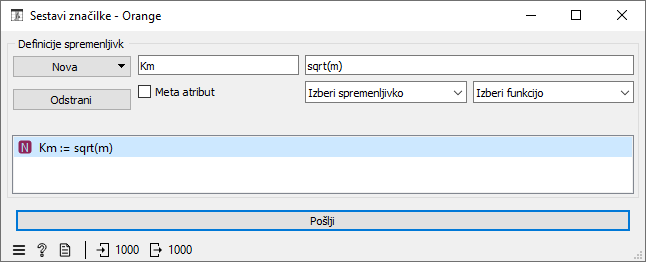
Vidimo, da odvisnost izgleda podobna korenski funkciji, zato bomo dodali nov atribut, ki bo enak korenu mase uteži, torej Km = √(m). Če sedaj s polinomsko regresijo modeliramo nihajni čas t v odvisnosti od novega atributa Km, bomo veliko bolj uspešni. Tako pridemo do enačbe t = 0,00 + 1,41 * Km.

Do sedaj smo iskali odvisnost nihajnega časa od enega samega atributa, na voljo pa jim imamo več. Kaj pa, če bi upoštevali več atributov hkrati in poiskali koeficiente a (a₀, a_Km, a_m, a_d), ki bi čim bolje modelirali nihajni čas z enačbo t = a₀ + a_Km * Km + a_m * m + a_d * d.

Temu je namenjena linearna regresija, ki odkrije enačbo t = 0,05 + 1,39 * Km + 0,00 * m + 0,02 * d. Če primerjamo uspešnost (RMSE) polinomske regresije in linearne regesije z uporabo gradnika Testiraj in meri, bomo videli, da imata praktično enako uspešnost. Zato bomo majhne koeficiente brez večje škode igorirali. Tako smo sedaj dobili enačbo t = 1,39 * √m.

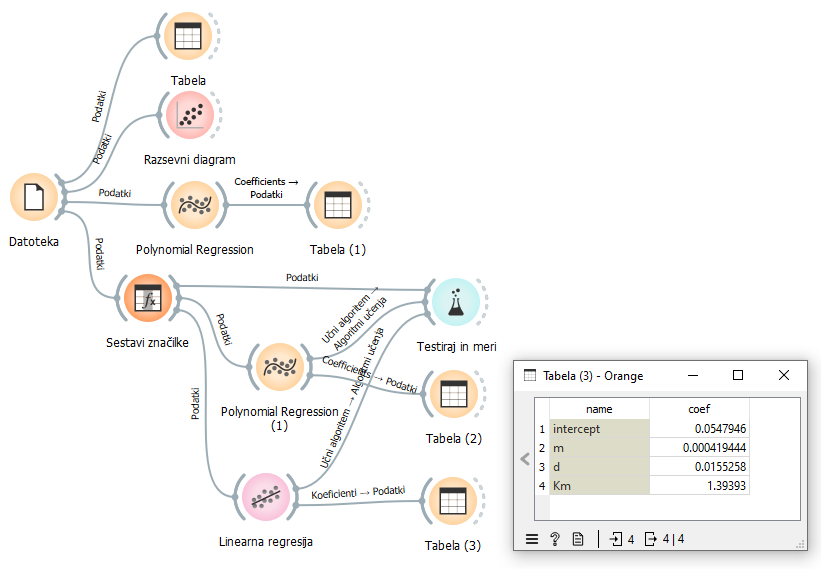
Različne vzmeti

Iz prejšnjega rezultata lahko sklepamo, da je nihajni čas neodvisen od raztezka d, zato ga v nadaljevanju ne bomo uporabljali. Podatke lahko damo linearni regresiji in dobimo izhodiščno odstopanje RMSE = 1,415, ki ga bomo poskusili zmanjšati. Če bi lahko idealno modelirali nihajni čas, bi bil RMSE enak 0, vendar to ne bo mogoče že zaradi merskih napak v naših podatkih.

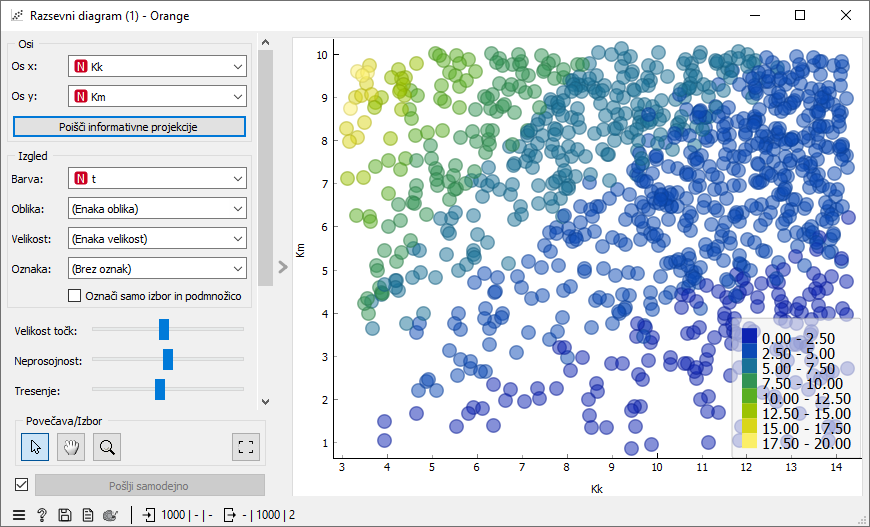
Prav tako vemo, da se je dobro obnesel koren mase, zato dodajmo še koren koeficienta vzmeti in si oglejmo podatke v razsevnem diagramu. Tokrat opazujemo odvisnost časa od dveh spremenljivk Km = √m in Kk = √k. V diagramu bomo zato čas predstavili z barvo. Opazimo lahko, da je nihajni čas večji pri večjih masah in pri manjših koeficientih uteži. Dosti več pa iz tega ne moremo sklepati.

Dajmo sedaj vse atribute linearni regresiji, da poišče koeficiente, s katerimi bi čim bolje modelirala čas, in preverimo njeno uspešnost. Z enačbo t = 13,11 + 0,00 * m + 0,09 * k + 0,75 * Km - 2,31 * Kk doseže RMSE = 0,846, kar je že napredek v primerjavi z našim prvim poskusom (RMSE = 1,415). Dodatek korenov torej pomaga pri modeliranju. V razsevnem diagramu lahko primerjamo dejanski nihajni čas in napovedano vrednost. Če bi bile naše napovedi zelo točne, bi pričakovali vse točke na diagonali (na sliki označeni z rdečo). Vendar opazimo, da temu ni povsem tako. Predvsem pri večjih nihajnih časih, model precej zgreši. Na drugi strani pa so pri majhnih nihjanih časih nekatere napovedi celo negativne!

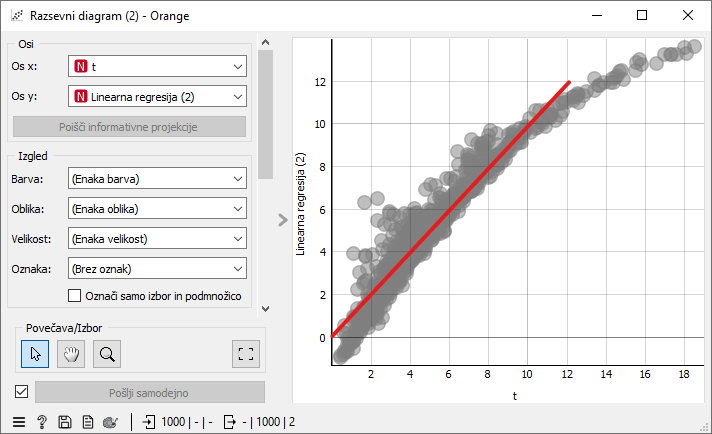
Če nas zanima samo napovedovanje nihajnih časov, lahko uporabimo enostaven pristop napovedovanja z najbližjimi sosedi. Za podane atribute (maso in koeficient uteži) poiščemo nekaj najpodobnejših primerov (npr. 5) in napovemo njihovo povprečno vrednost. S tem pristopom smo veliko natančnejši, vendar nam ne koristi pri interpretaciji. Iz takega modela ne moremo sklepati nič novega o fizikalnem procesu iz podatkov.

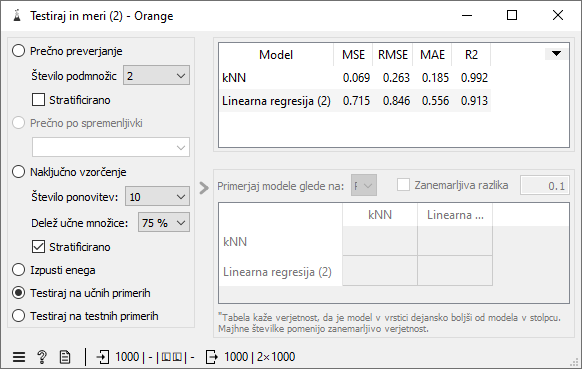
Logaritmi

Iz izkušenj vemo, da iskana enačba najbrž ni linearna kombinacija oblike (1), kjer so x₁, x₂, … naši atributi, ampak bo nek produkt potenc oblike (2), kjer iščemo koeficiente c, a₁, a₂, … Na voljo imamo linearno regresijo, ki je sposobna poiskati koeficiente v enačbi prve oblike, zanimajo pa nas koeficienti v enačbi druge oblike. Pri tem si lahko pomagamo z logaritmi. Logaritmirajmo obe strani enačbe (2), da dobimo enačbo oblike (3), in jo zapišimo z novimi spremenljivkami (4), ki predstavljajo logaritme atributov. Koeficiente v tej novi enačbi pa lahko poiščemo z linearno regresijo. Imamo torej orodje, ki je sposobno modelirati logaritme atributov, s katerimi delamo. Z uporabo linearne regresije izračunamo koeficiente C, a₁, a₂, … v enačbi (4), nato pa moramo vse skupaj pretvoriti nazaj. To naredimo z uporabo eksponentne funkcije (5) in dobimo končno obliko (6). (Opomba: c = e^C)

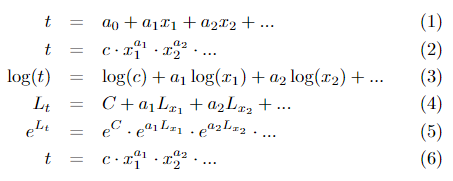
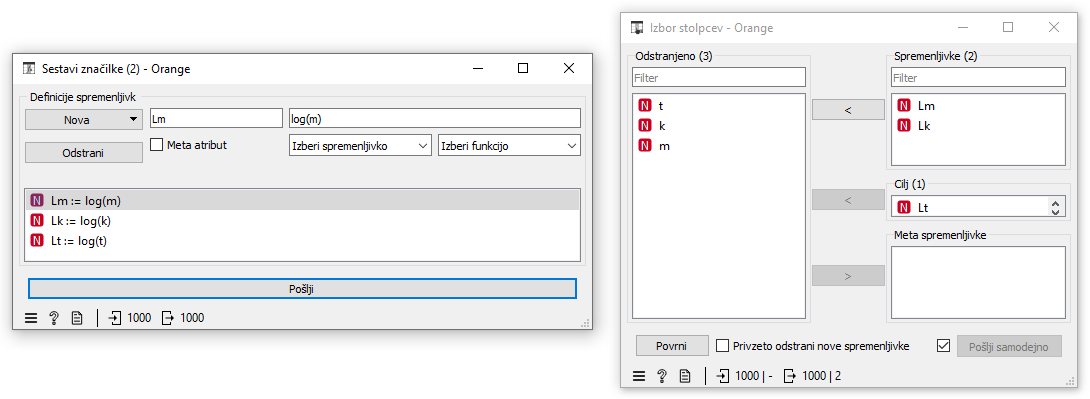
Z gradnikom Sestavi značilke sestavimo nove atribute, ki so logaritmi obstoječih, in nato z gradnikom Izbor stolpcev izberemo samo nove atribute, da ne bomo imeli mešanice logaritmiranih in nelogaritmiranih atributov. Z uporabo linearne regresije lahko sedaj dosežemo RMSE = 0,065, ki je zelo blizu ničle, kar predstavlja skoraj popolno ujemanje modela z dejanskimi vrednostmi. Vendar te vrednosti RMSE ne smemo primerjati s prejšnjimi! Sedaj namreč modeliramo logaritme vrednosti. Če uporabimo koeficiente, ki jih je odkrila linearna regresija, dobimo enačbo t = e^1.838 * m^0.502 * k^-0.503.

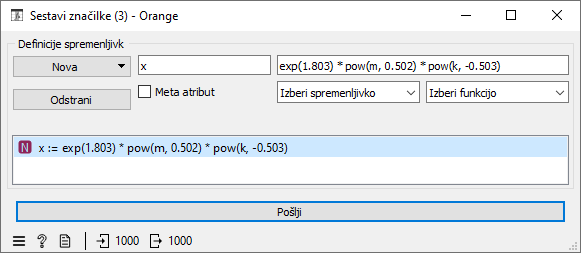
Sedaj lahko sestavimo novo spremenljivko x, ki bo predstavljala našo napoved z uporabo prej odkrite enačbe. Za namene preverjanja natačnosti napovedi pa izmed atributov izberimo samo našo napovedno spremenljivko in z uporabo polinomske regresije preverimo njeno uporabnost. Dobimo RMSE = 0,199, ki je precej boljši od naših prejšnjih poskusov (1,415 in 0,846). Če pogledamo polinomsko regresijo, ta praktično ne spremeni naše napovedne spremenljivke.

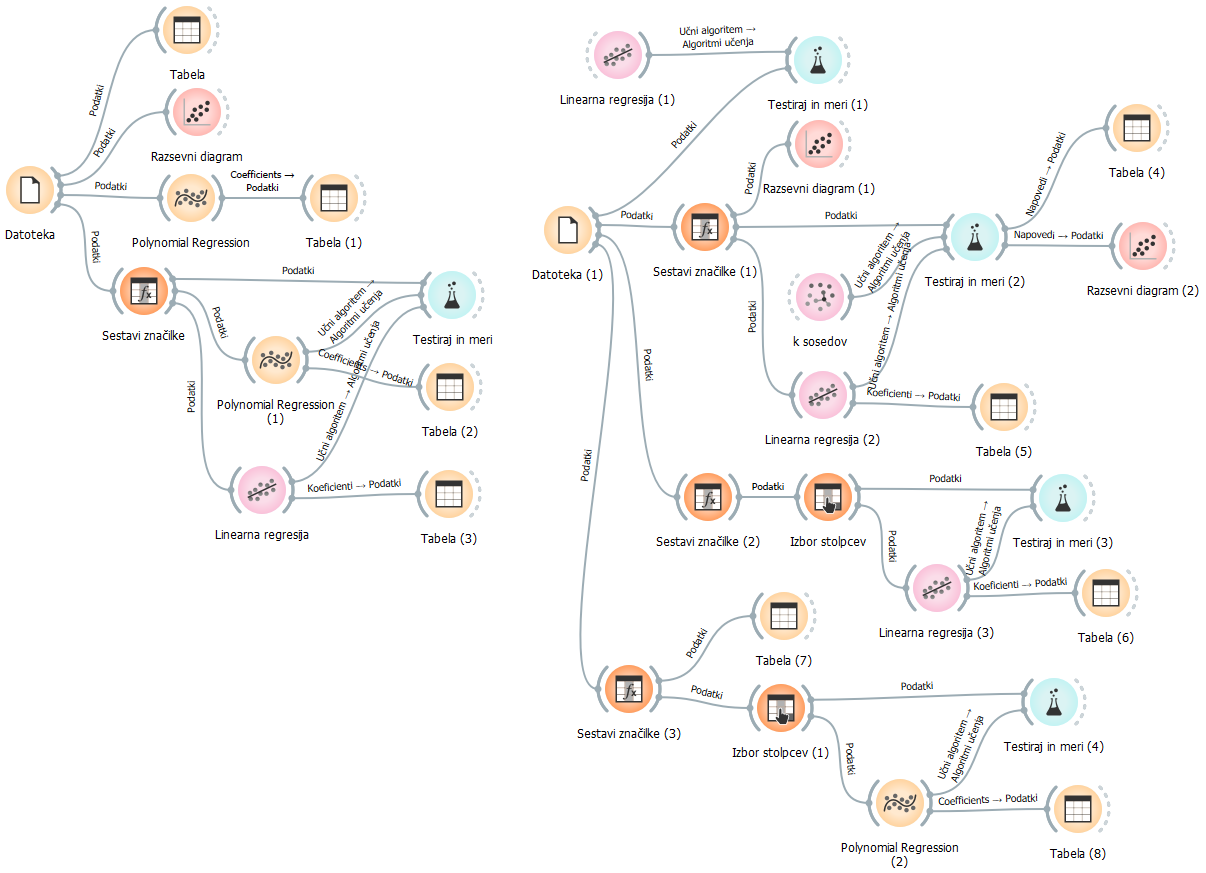
Pri reševanju našega problema smo sestavili kar impresiven delotok.

Zaključek

Kaj pravijo o vzmetnem nihalu tisti, ki obvladajo fiziko? Spodaj je navedena pravilna enačba nihajnega časa za vzmetno nihalo in njene drugačne oblike za primerjavo z odkritimi enačbami. Če naše odkritje malo zaokrožimo in poenostavimo, dobimo t = 6.28 * √m / √k. Vidimo lahko, da smo bili z našimi približki zelo blizu pravim vrednostim kljub merskim napakam v podatkih.

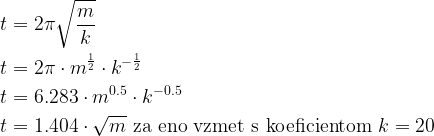
Oglejmo si še odgovore na začetna vprašanja, ki bi morali biti sedaj že jasni:

• Povečanje mase poveča nihajni čas. Da premaknemo oz. zanihamo predmet z večjo maso, traja dlje časa.
• Povečanje koeficienta vzmeti zmanjša nihajni čas. Trša kot je vzmet, hitreje zaniha utež tja in nazaj.
• Začetni odmik nima vpliva na nihajni čas. Vsaj ne v primeru idealne vzmeti s koeficientom, ki ni odvisen od raztezka.

Enak poskus bi lahko izvedli tudi za navpično pritrjeno vzmetno nihalo, saj zanj veljajo enake lastnosti, le da je začetna ravnovesna lega zaradi gravitacije malo drugačna.