
How Do You Call This Quadrilateral?
The end of the school year is approaching fast, and teachers are already thinking how to get kids excited about what they will be learning next year. For example, quadrilaterals.
In the 6B grade of the Alojzij Šuštar Primary School, thev students already know the basics of quadrilaterals – they know for example that a square and a rectangle both have interior right angles, and that a square has sides of equal length. They also know how to draw some geometric shapes that don’t have right angles, although the names of those are slightly more elusive (deltoid, rhombus, and a parallelogram). About a rhombus and a parallellogram, they can tell you that their sides are parallel, and in the case of a rhombus, even of equal length. And that a deltoid looks like a kite.
Once we revised the quadrilateral fundamentals, the students got divided into eight groups. Each group was given five geometric shapes whose characteristics they needed to determine: are all their sides of equal length, do they have two pairs of equal sides, are all their angles right angles, and so on. The students entered the data in a common spreadsheet.
We then imported this data into Orange, built a decision tree and – ta daaam, a scheme depicting the characteristics of quadrilaterals was produced. It looked something like this:
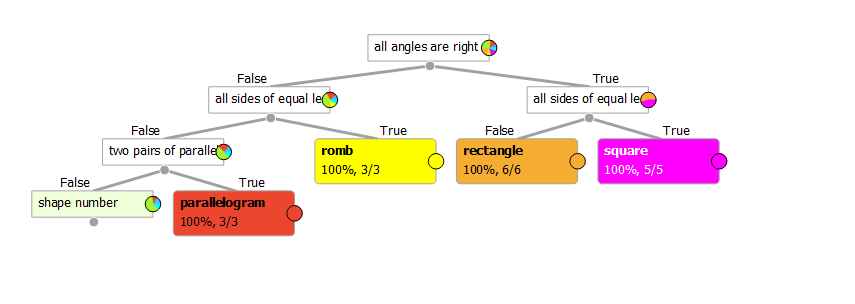
The decision tree produces a pattern it has identified from the data. How accurate is the tree?
A computer is clearly capable of autonomously identifying geometric shape types, providing we supply it with the right data from which it can learn the patterns. Since the students’ data included some typographic errors, the errors also appeared in the tree. That gave us a perfect opportunity to have a conversation on the meaning of good quality data, and how our model for identifying geometric shapes will only be as accurate as the data it is fed.
On our website, you can find a more detailed description of the activity.