Clusters in the Classroom

It often makes sense to observe data by grouping them, for example, by finding groups of similar countries, images or people. The popular hierarchical clustering can be experience with a kinesthetic activity described here. To lead somewhere, it can be followed by one of activities in which we cluster real data.

Preparation of “data”

1. Draw the axes of the scatter diagram on the floor of the classroom or a suitably sized room (you will need about 3x3 metres) using masking tape. If we don’t have tape, we will just wave around a bit more.

2. We will place the students in a scatter diagram according to their math knowledge and football skills. We can give them random names, but we arrange them in such a way that we get three groups and a lone student. (Let’s make it fun: we declare a typical football player a mathematician, or vice versa. Of course, let’s make sure we don’t offend anyone.)

   
   

   (Same image with German and French names)

   

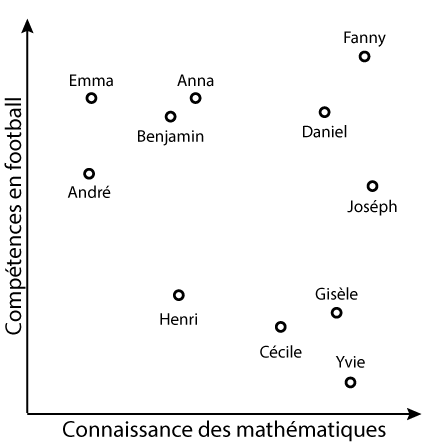
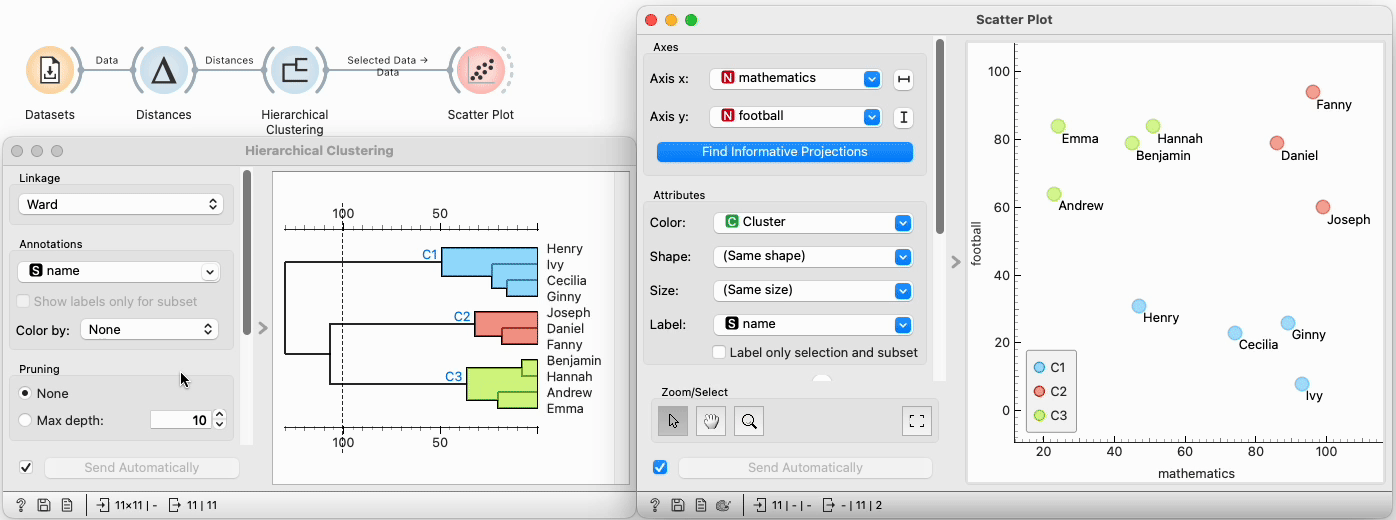
   In the example above, we have two excellent footballers, Emma and Hannah, with Emma not being particularly good at math but Hannah not being much better either. Fanny, for example, excels at both. Ivy, on the other hand, is an excellent mathematician with two left feet for football.

3. We ask the students: if you had to divide your classmates into groups based on their soccer and math skills, how many groups would there be? Probably three: soccer players, math whizzes, and those who are good at both. And then there’s Helga, who isn’t particularly good at either.

4. How would we determine the groups using a computer? A computer can’t just “see the groups”—it needs a process. Depending on the students’ age and level of computer knowledge, they might be able to come up with an algorithm—or maybe not. :)

Clustering process

The below text describes the process for the specific arrangement from the image above. In the classroom, the names will be different, but the process will be the same.

1. We start by treating each student is a group on their own.

2. In the first step, we will group the two students who are most similar. Using a tape measure, we measure the distances (at least between those who are a little closer, for example Ginny and Cecilia, Ginny and Ivy, and Hannah and Benjamin). Hannah and Benjamin are the closest, so they will be in the same group. To remember this, Hannah puts her hand on Benjamin’s shoulder.

3. In the next step, we again search for the nearest pair. We measure and find that it is probably Ginny and Cecilia. Ginny puts her hand on Cecilia’s shoulder.

4. The next closest couple are Ginny and Ivy. So Ginny will put her hand on Ivan’s shoulder (or vice versa). That makes three students in this group.

5. We continue to do so. Sometimes we merge individuals, sometimes we add individuals to groups, later we merge whole groups. It can get a bit tricky with the hands; it may happen that the person who is supposed to join the groups has both hands already occupied. Reorganize; instead of Ginny having her hand on Ivy’s shoulder, Ivy puts her on Ginny’s shoulder, freeing on of Ginny’s hands. Hands cannot run out.

6. Keep doing this as long as you can - either until the end, or until the arms get too short. Both are appropriate for explaining the algorithm. If we go to the end, we explain that we have obtained a hierarchy of groups. If we finish a little earlier, we say that the grouping stops when the groups get too big.

How does a computer do this?

If we want, we can also show how the computer performs this process.

1. 

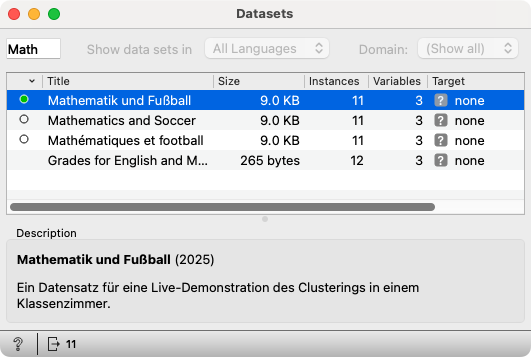
   Open the prepared workflow for Orange. (For the data with French or German names, open the Datasets widget, type “Math” in the filter box at the top left and double-click the corresponding dataset.)

2. Open the Hierarchical Clustering and Scatter Plot widgets. Arrange the windows so that both are visible.

3. 

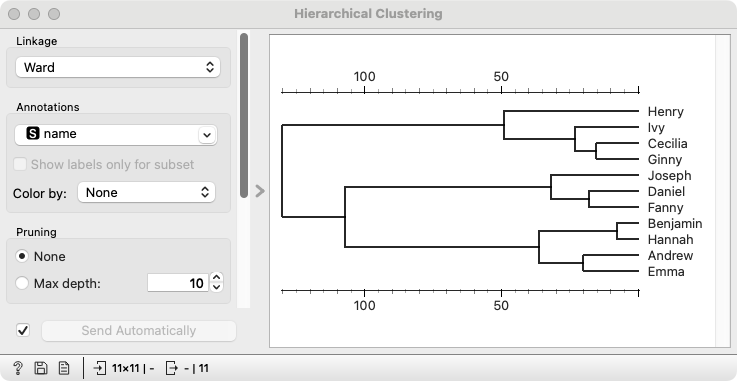
   The Hierarchical Clustering widget already displays a dendrogram, showing how groups merge. We read it together from right to left: the closest pair is Hannah and Benjamin, followed by Cecilia and Ginny, then Daniel and Fanny, and Andrew and Emma. Next, Ivy joins Ginny and Cecilia, and so on, until only one group remains.

4. We can also demonstrate the merging step by step. In the Hierarchical Clustering widget, set “Top N” (found in the lower left section) to 11, the number of students. In the scatter plot, we see that each student is initially in their own group.

5. We check who is most similar—Hannah and Benjamin, as we already know. We reduce the number of groups to 10 and see that clustering indeed merges them into one.

6. We continue checking which students are most similar… and repeat the process step by step.

   

Overlooked Details

During the live demonstration, we brushed over some details, and we also skipped them in the computer-based demonstration.

For measuring distances, we simply used “straight-line distance.” In practice, there are different ways to define distance, and we also need to be mindful of normalization. If the data have different measurement scales (e.g., height in meters ranging from 1 to 2, while weight in kilograms ranges from 30 to 100), they need to be adjusted accordingly so they are comparable. Similarly, categorical variables, such as eye color, need to be handled appropriately.

Another important detail is the distance between groups. How far apart are two groups? Do we measure the distance between their closest members or their most distant members? Or do we calculate the average distance? The function that defines the distances between groups is called the linkage function. In our demonstration, we measure the closest distance. However, in practice, a more complex definition is often used—one that is somewhat similar to the average distance but not exactly the same.