Prepoznavanje štirikotnikov

Bistvo ure je ponavljanje različnih vrst štirikotnikov in različnih lastnosti. Računalnik doda nekaj zabavne komponente (vnašanje podatkov), predvsem pa omogoča, da vidimo in skupaj analiziramo napake, ki jih naredijo učenci. Če ne želimo zaiti globlje v umetno inteligenco in strojno učenje, se lahko ustavimo tu. Zanimivo pa je iti naprej: računalnik lahko sam sestavi pravila, ki jih lahko opazujemo, preverjamo. Mimogrede vidimo, kako je model, narejen iz delno napačnih podatkov, tudi sam (navadno) delno napačen.

Uvod

V uvodu ponovimo različne vrste štirikotnikov (rišemo na tablo, rišejo jih oni…) in se spomnimo na lastnosti, s katerimi so definirani (vzporedni pari stranic, pravi koti…). Učence poskušamo pripeljati do tega, da oblikujejo pravila za razlikovanje med njimi. Lahko jih tudi zapišemo.

Vprašamo jih, ali bi zmogel računalnik sam odkriti ta pravila, če bi mu pokazali dovolj različnih vrst štirikotnikov.

Aktivnost je mogoče izvesti tudi, če teh likov še ne poznajo. Lahko jih, na primer, prosimo, da opišejo pravokotnik. Če povejo, da “ima po dve stranici enako dolgi”, narišemo nekaj “pravokotnikov”, a med njimi tudi paralelogram; počakamo, da ugovarjajo in prosimo, da povedo natančnejšo definicijo pravokotnika.

Like pustimo narisane na tabli, da se bodo učenci manj motili.

Aktivnost zahteva vsaj pol ure. Če smo omejeni na 45 minut, za ta, uvodni del, ne smemo porabiti preveč časa.

Priprava podatkov

Razred razdelimo na 5-6 skupin. Vsaka skupina bo razvrstila del štirikotnikov.

Odpremo stran za vnos podatkov: na strani https://data.pumice.si/stiri, vnesemo število skupin in po pritisku na gumb dobimo povezavo za vnos podatkov. Povezavo vpišemo na naprave (tablice, računalnike), s katerimi bodo učenci vnašali podatke, ali pa to prepustimo učencem. Vsaka skupina si izmisli in vnese svoje ime. Lahko jih tudi omejimo, recimo, na imena po živalih, na primer jazbeci, volkovi…

Na naslednjih straneh bodo morali vnašati lastnosti štirikotnikov in določati njihova imena. Učence opozorimo, da morajo vnašati najbolj specifično vrsto lika. Če gre za pravokotnik, naj vnesejo pravokotnik in ne paralelogram ali trapez, čeprav je vsak pravokotnik tudi paralelogram in trapez.

Opazovanje napak

Zbrane podatke odpremo v gradniku Datoteka, tako da v polje URL vpišemo povezavo, ki jo dobimo na strani. (Če jo pozabite: enaka je povezavi, na kateri so učenci vnašali podatke, le na konec dodamo še /data). Če tole berete doma, ker želite povaditi, pa vnesite URL strani s simuliranimi podatki, https://pumice.si//aktivnosti/stirikotniki/resources/stirikotniki.tab.

Dobljena tabela (če jo želimo pogledati, povežemo Datoteka s Tabela) je takšne oblike:

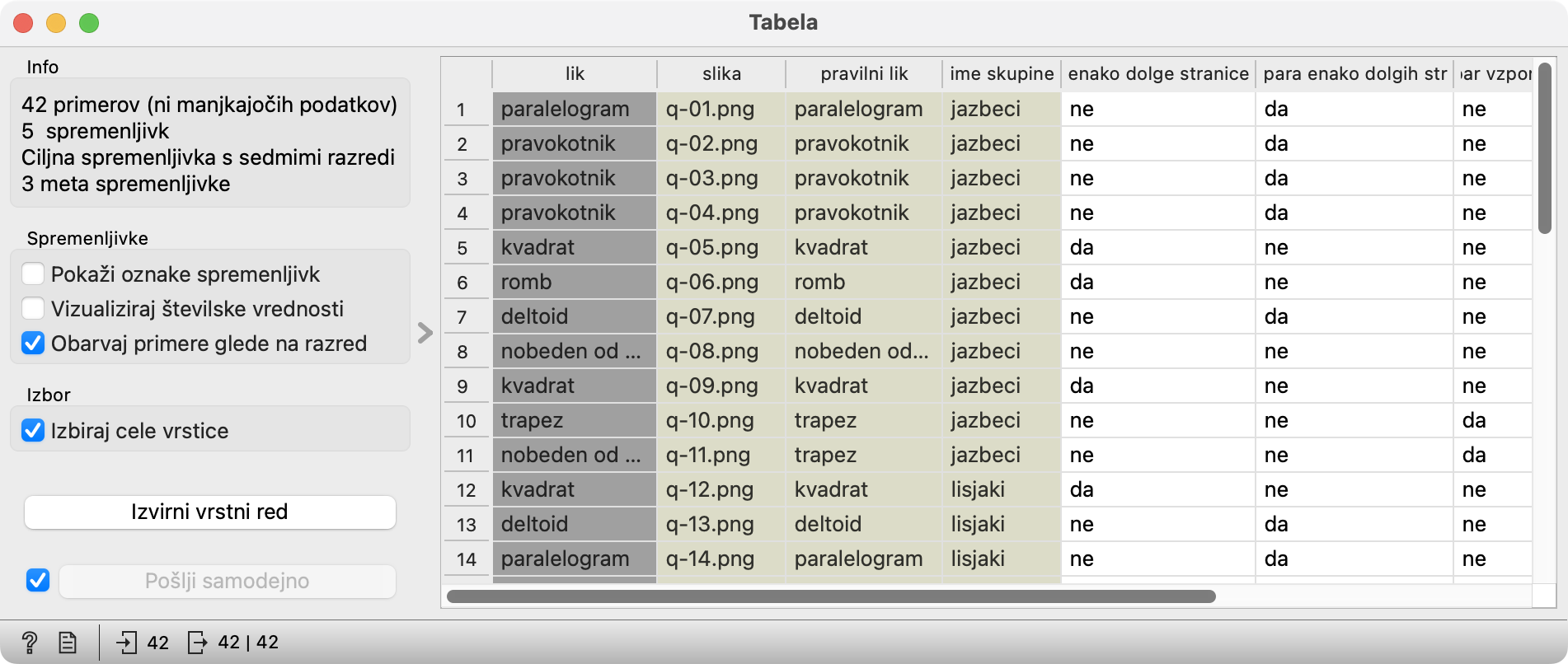
Stolpec “lik” vsebuje odgovore učencev, stolpec “pravilni lik” pa pravilne razvrstitve likov. Stolpec “ime skupine” pove, katera skupina je razvrščala določen lik. Sledijo stolpci z lastnostmi likov.

Zanimivo bi bilo pogledati, pri katerih likih so se učenci zmotili. Za to povežemo Datoteka s Pivotna tabela. V Pivotni tabeli nastavimo vrstice na “lik” stolpce pa na “pravilni lik”. Tako bomo videli, kje so se učenci največkrat zmotili.

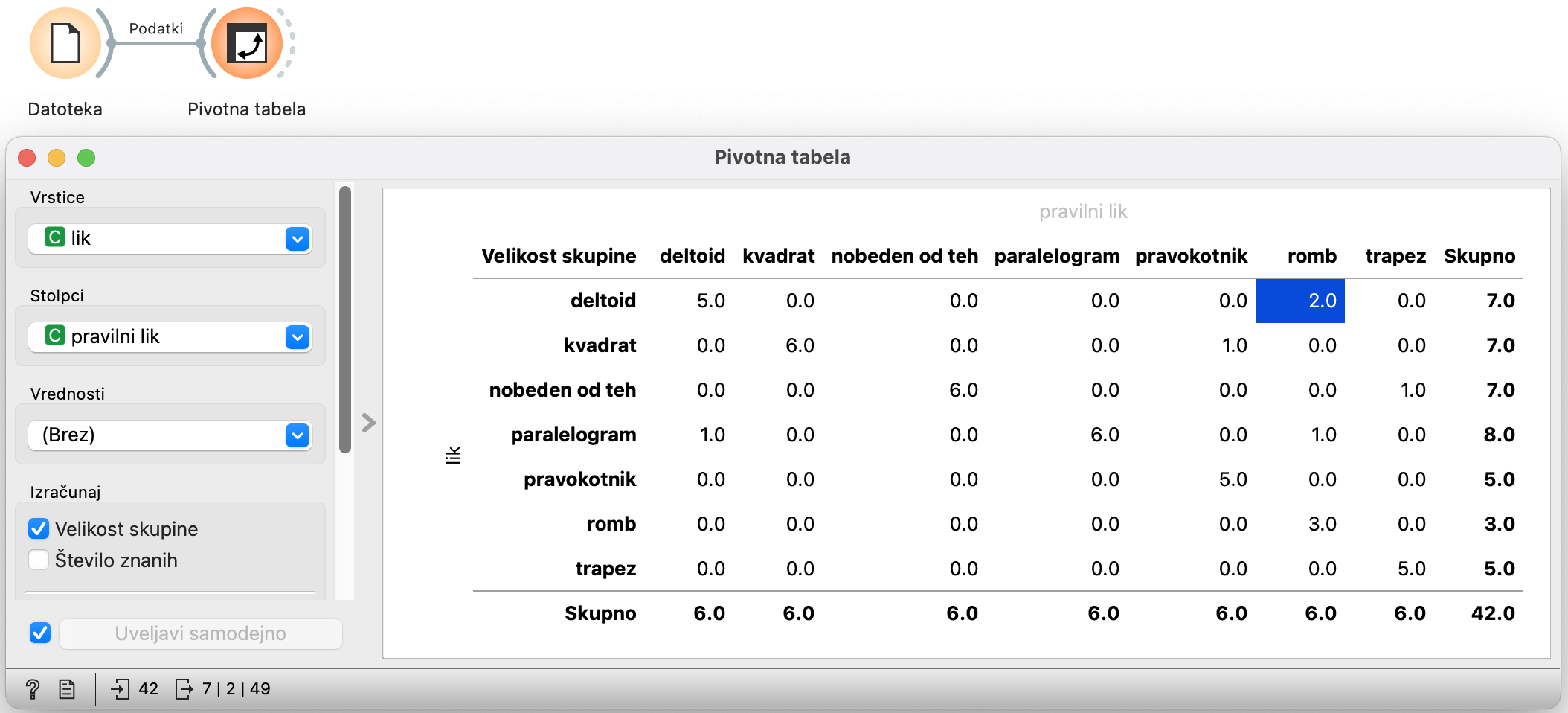
Gornja tabela, na primer pove, da sta dva romba nepravilno uvrščena med deltoide (označeno polje). Poleg tega je en romb postal paralelogram (polje tri vrstice nižje), en pravokotnik pa kvadrat. En trapez ni bil prepoznan kot nič posebnega, pa še en deltoid je bil prekrščen v paralelogram. Vse številke na diagonali pa predstavljajo pravilne uvrstitve.

Napake je seveda zanimivo videti. Pivotno tabelo priključimo na Pregledovalnik slik. Pivotna tabela ima več izhodov. Privzeti je Pivotna Tabela (tabelica s takšnimi številkami, kot jih kaže gradnik), tule pa bi radi kazali podatke, ki jih izberemo v tabeli, zato je potrebno prevezati izhod na Izbrani podatki.

Ko zdaj izberemo celico v pivotni tabeli, bomo v pregledovalniku slik videli pripadajoče slike. Če poleg tega nastavimo Stolpec z naslovom na Skupina, bomo videli tudi, katera skupina je naredila napako in jo izzvali, naj jo najde. Sodeč po spodnji sliki skupina, ki si je nadela ime “veverice” ne prepoznava rombov (morda zato, ker niso narisani tako, da je en par stranic vodoraven?) in jih “degradira” v deltoide.

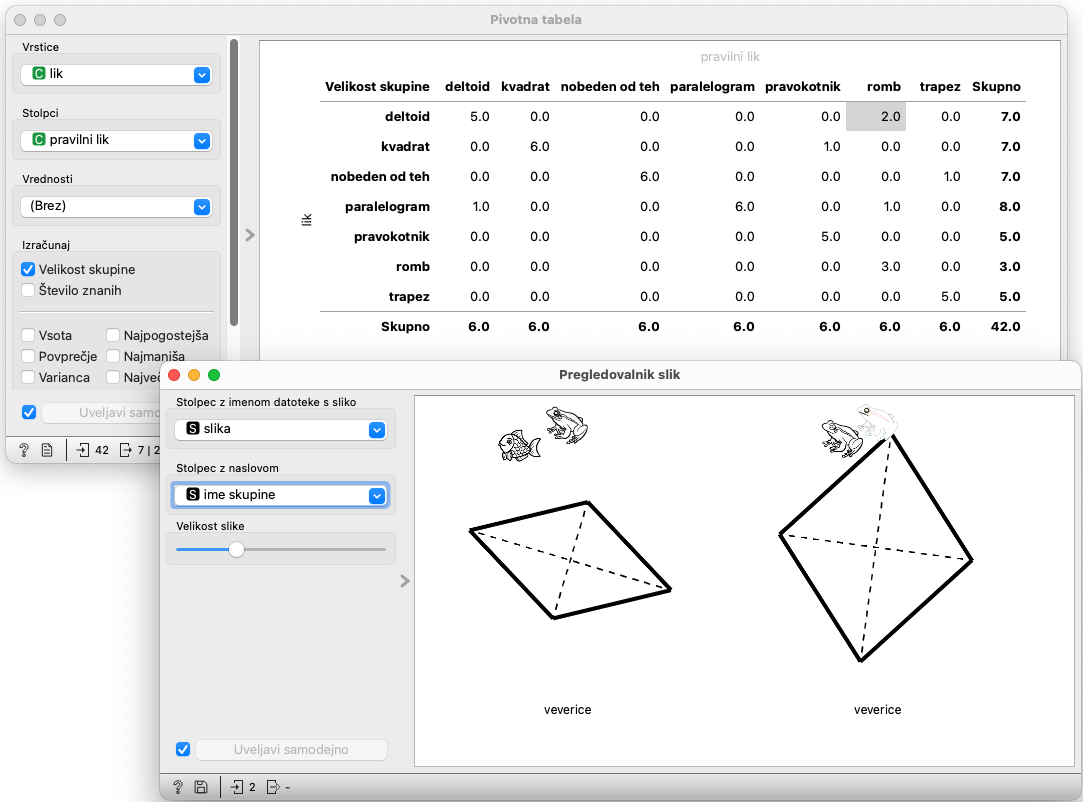
Pivotno tabelo lahko povežemo tudi z gradnikom Tabela (spet ne smemo pozabiti prevezave signalov!), pa bomo lahko za vse like, ki jih izberemo v Pivotni tabeli, videli podatke, ki so jih vnesli učenci in raziskali ali so poleg imena zgrešili tudi katero od njegovih lastnosti.

Gradnja odločitvenega drevesa

Datoteko povežemo z gradnikom Drevo, ki zgradi drevo. V njem pobrišemo vse kljukice. (Te izbire ustavljajo sestavljanje drevesa, ko algoritmu začne zmanjkovati podatkov, da bi lahko zanesljivo določal nova pravila. Tu to izključimo, ker je podatkov tako ali tako premalo, poleg tega pa nas zanimajo prav napake v drevesu.)

Idealno drevo je takšno.

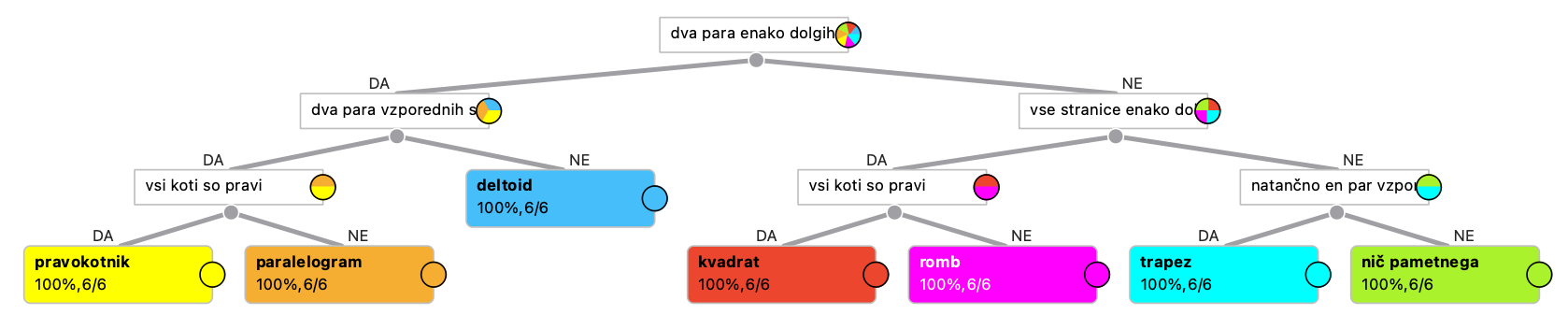
Ker bodo učenci pri opisovanju in razvrščanju likov delali napake, bo drevo iz njihovih podatkov verjetno bolj zapleteno in nepravilno. To je dobro, saj bomo lahko opazovali povezavo med napakami učencev in dobljenim modelom.

Razložimo, kako je potrebno brati drevo in preverimo, ali pravilno opisuje vrste štirikotnikov. Na primer: če ima dva para enako dolgih stranic, nima pa dveh parov vzporednih stranic, gre za deltoid.

Če je dobljeno drevo tako nepravilno, da je neuporabno, pa lahko za njegovo gradnjo uporabimo pravilnejše podatke:

• Ena možnost je, da V gradniku Datoteka v tabelici v spodnjem delu poiščemo “lik”; tam kliknemo “ciljna” in spremenimo v “meta”. Nato poiščemo vrstico “pravi lik” in spremenimo “meta” v “ciljna”. Kliknemo Uveljavi. Tako bomo dobili drevo, ki je zgrajeno iz likov, ki so pravilno razvrščeni, njihove lastnosti pa so še vedno takšne, kot so jih vnesli učenci. Če so učenci pri nekam pravokotniku pozabili označiti, da ima prave kote, se bo v neki veji drevesa, ki se nanaša na like z ne-pravimi koti pojavil tudi pravokotnik.

• Druga možnost je, da uporabimo podatke z naslova https://pumice.si//aktivnosti/stirikotniki/resources/stirikotniki-pravilni.xlsx. Z njimi bi morali dobiti takšno drevo, kot je na zgornji sliki.

Učencem lahko pokažemo nekaj novih likov (ali jih narišemo na tablo) in vprašamo, kakšen lik je to. Pri tem uporabimo drevo, da določimo tip lika.

Če želimo, lahko pokažemo tudi, kako računalnik uporabi drevo za napovedovanje. Na platno postavimo nov gradnik Datoteka in vanj naložimo podatke z nekaj štirikotniki ( https://pumice.si//aktivnosti/stirikotniki/resources/stirikotniki-neznani.xlsx). Gradnik povežemo z gradnikom Napovedi, tako da bo določal vrste likov v teh podatkih. Gradnik Napovedi potrebuje tudi napovedni model, zato povežemo Drevo z Napovedi.

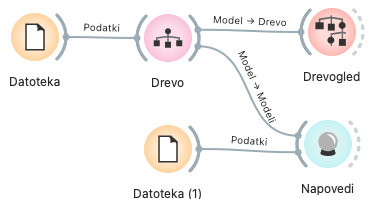
Odpremo Napovedi in … preverimo opise likov in napovedi. So pravilne?

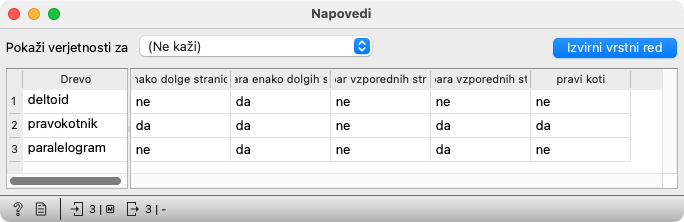
To vajo je smiselno ponoviti s podatki, ki so jih pripravili učenci in s pravimi podatki (točka 2, zgoraj). Če vsebujejo podatki učencev preveč napak, pa seveda le s pravilnimi.

Opazovanje napak drevesa

Drevo, ki ga dobimo iz podatkov učencev, bo morda videti takole (tole je sicer drevo, sestavljeno iz simuliranih napačnih podatkov).

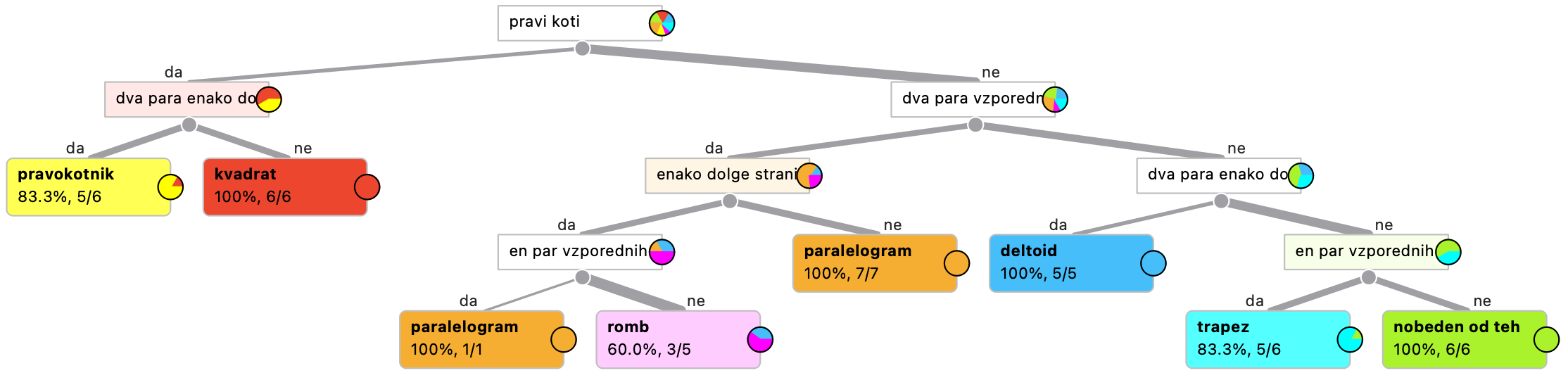
Nekatera pravila so očitno napačna: čisto levo imamo šest likov, ki imajo prave kote in dva para enako dolgih stranic (ta možnost se v obrazcu izključuje z možnostjo, da so vse stranice enake), vendar je eden od njih kvadrat. To je seveda narobe.

Znamo odkriti, zakaj se je računalnik zmotil? Drevogled povežemo s Pregledovalnikom slik in s Tabelo. V drevesu kliknemo ta “list” in v Pregledovalniku slik vidimo teh šest likov.

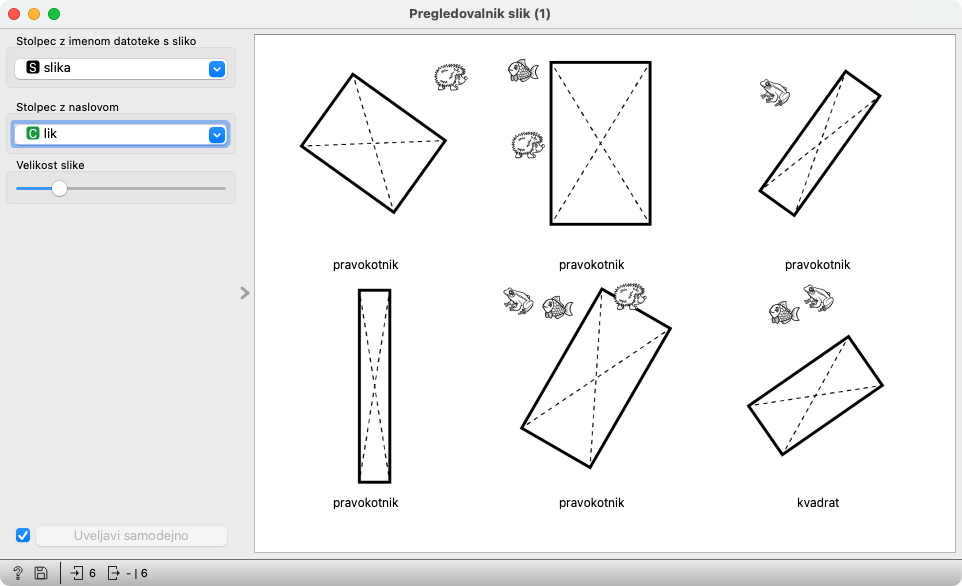
Aha! Liki so očitno pravilno opisani (sicer se ne bi znašli v istem listu drevesa), vendar je eden od njih napačno oklican za kvadrat. (Ni čudno; tudi odrasli pravokotnikom pogosto rečemo kar kvadrati, saj je … preprosteje. :)

Podobno si lahko ogledamo druge like. Včasih bo lik pravilno uvrščen, vendar narobe opisan. To najlažje vidimo v tabeli.

Razširitev: nepomembni atributi

Če ob sestavljanju strani vključimo vprašanja o živalih, ki se pojavljajo na slikah, bodo tudi odgovori nanje v tabeli s podatki. Živali so razporejene tako, da v resnici ne nosijo nobene informacije: ježek se enako pogosto pojavi ob vsaki vrsti lika.

Če so vsi podatki pravilni, se živali ne bodo pojavile v drevesu: ne ježki, ne ribe ne žabe ne plezajo. Algoritmi strojnega učenja načelno znajo razlikovati med pomembnimi in nepomembnimi, uporabnimi in neuporabnimi podatki.

Če so v podatkih napake, pa se bo zgodilo, da bosta pred algoritmom učenja dva lika, na primer paralelogram in kvadrat (glede na razvrščanje učencev, seveda!), ki bosta imela popolnoma enake lastnosti, le da bo na eni sliki tudi žaba, na drugi pa ne. V tem primeru bo algoritem učenja verjetno ugotovil, da je prisotnost žabe pomembna za razlikovanje med kvadratom in paralelogramom…

Temu se učeno reče “šum v podatkih”, po domače: napake. Napake prepoznamo po tem, da so “nenavadne”: če imamo šest likov z enakimi lastnostmi, med katerimi je pet rombov in en deltoid, lahko sklepamo, da je romb napačno razvrščen, zato ga zanemarimo. Če tega ne storimo, rečemo, da se je model preveč prilagodil podatkom (overfitting). Proti temu nas varujejo prav tiste možnosti, ki smo jih v gradniku Drevo izključili. To smo storili, ker smo želeli videti napake.

Diskusija ob koncu

Kdaj lahko za neko napravo rečemo, da je pametna, inteligentna? Je pametni telefon res pameten? Zakaj? Ker nas opozori na rojstne dneve prijateljev - če mu povemo zanje? Je to res “pamet”? Za to je zgolj sprogramiran.

Lahko rečemo, da je računalnik inteligenten, če se nauči nekaj, česar prej ni znal: naučil se je razlikovati med štirikotniki - sam, na osnovi primerov. Zanimivo je tudi to, da je odkril (če ga niso zavedli napačni podatki), da so podatki o živalih, dorisanih na listih, nepomembni.

Je torej naredil nekaj za kar ni bil sprogramiran? Da in ne. Ni bil sprogramiran za razlikovanje likov. “Sprogramiral” se je sam. Bil pa je sprogramiran za to, da se uči - da se “samoprogramira”. Je potem pameten ali ne? Ali je potem res pameten ali ne, je stvar pogleda.

Za konec učencem povemo, da se napovedni modeli dandanes uporabljajo vsepovsod. V medicini, na primer, računalniku pokažemo večje število ljudi z različnimi simptomi in mu povemo, katero bolezen imajo; tako se računalnik nauči na podlagi simptomov prepoznavati bolezni, čisto tako, kot se je na podlagi lastnosti štirikotnikov naučil prepoznavati njihove vrste.