Priporočilni sistem za risanke

Priporočilne sisteme srečujemo vsepovsod. Odrasli jih videvamo, recimo, v spletnih trgovinah, učenci pa jih morda najprej srečajo na straneh z videoposnetki, kot sta YouTube in Tiktok. V tej učni uri izvemo, kako takšni sistemi delujejo. Ura je privlačna zaradi teme, saj morajo učenci izbirati morajo svoje najljubše risanke ali glasbenike. Uro lahko zapeljemo tudi tako, da govorimo o tem, kako nas tovrstni sistemi, ki ne služijo le priporočanju video posnetkov, temveč tudi novic in objav na družbenih medijih, ujamejo v mehurčke in nam prikažejo le tisto, kar že poznamo in nam je všeč.

Ura ima matematično ozadje. Če jo izvajamo s starejšimi učenci, lahko vključimo množice (preseki, unije); z mlajšimi računamo velikosti presekov, čeprav ne uporabljamo nujno teh izrazov. Učenci narišejo tudi graf podobnosti, nekakšen sociogram, oziroma “okusogram”.

Prvi del ure poteka v skupinah: vsaka skupina sestavi priporočila, ki temeljijo na izborih članov skupine. Nadaljujemo lahko tako, da svoje izbore vnesejo prek spletne strani in dobimo priporočilni sistem iz podatkov vsega razreda. V takšni izvedbi aktivnost vzame dve šolski uri. Če jo želimo skrajšati, prvi del preskočimo in učenci že takoj vnašajo podatke v računalnike, vendar je ura v tej obliki manj zabavna in tudi manj poučna, saj sistema ne sestavijo sami, temveč ga zgolj opazujejo.

Učenci v aktivnosti uživajo: všeč jim je izbiranje risank ali serij, zanimivo jim je računanje podobnosti in risanje grafov. V komentarjih na koncu ure pa so povedali tudi, da jim je všeč, da zdaj vedo, kako (približno) delujejo takšne spletne strani.

Uvod

Za uvod se z učenci pogovorimo o tem, ali gledajo spletne strani z videi in kako jim te strani, po njihovem mnenju, priporočajo videe. Najbrž bodo povedali, da jim stran “pač priporoča posnetke, podobne tem, ki jih običajno gledajo”, po čemer jih vprašamo, na kakšen način stran ugotovi, ali so posnetki podobni. Če odgovorijo, da po opisih, lahko povemo, da so opisi pogosto kratki. Predvsem pa - kako primerja opise? Sta si dva opisa podobna, če vsebujeta podobne besede?

Obljubimo jim, da bomo pokazali, kako bi deloval sistem, ki se ne bi zanašal na opazovanje vsebine videov.

Priporočilni sistem v razredu

1. Učence razdelimo v skupine s približno 8 učenci. Vsaka skupina dobi list velikosti A3 in kartice s slikami risank; za vsako lahko natisnemo dva kompleta, tako da se vsaka risanka pojavi dvakrat. Vsak učenec dobi list papirja (zadoščal bo A5).

2. 

   Vsak učenec izbere 7 risank, ki so mu najbolj všeč. Na levo stran lista napiše njihove številke in imena. (Isto risanko lahko izbere poljubno število otrok. V razredu se je zgodilo, recimo, da so v neki skupini “punce pobrale vse ta najboljše risanke” in jih fantje zato niso mogli izbrati. :)

   Če aktivnost izvajamo s starejšimi učenci, lahko dovolimo različno število, recimo 6-9 risank. V tem primeru bo potrebno računati preseke in unije ter vaditi deljenje in decimalna števila. Detajli so opisani spodaj.

3. 

   Vsak učenec na list napiše na desno stran imena vseh ostalih članov skupine in zraven vsakega napiše, koliko enakih risank sta izbrala.

4. Vsak učenec obkroži tiste tri člane skupine, ki so izbrali največ istih risank kot on. Če si tretje mesto deli več učencev, izbere poljubne med njimi; na koncu naj bodo obkroženi le trije učenci.

5. 

   Skupina vzame list A3. Nanj napiše imena vseh članov skupine. Vsak član nariše puščice do tistih treh sočlanov, ki so mu najbolj podobni. Skupine lahko spodbudimo, da narišejo čim lepšo sliko - takšno, v kateri so tisti, ki so si bolj podobni, narisani bližje skupaj in tako, da se povezave čim manj križajo.

   Pomembno je, da ne povezujemo najbolj podobnih učencev, temveč vsak učenec nariše povezave do treh. Na ta način se izognemo temu, da bi bil kak učenec sam zase, brez povezav.

6. Vsak član skupine k svojemu imenu z modro barvo napiše številke risank, ki jih je izbral.

7. 

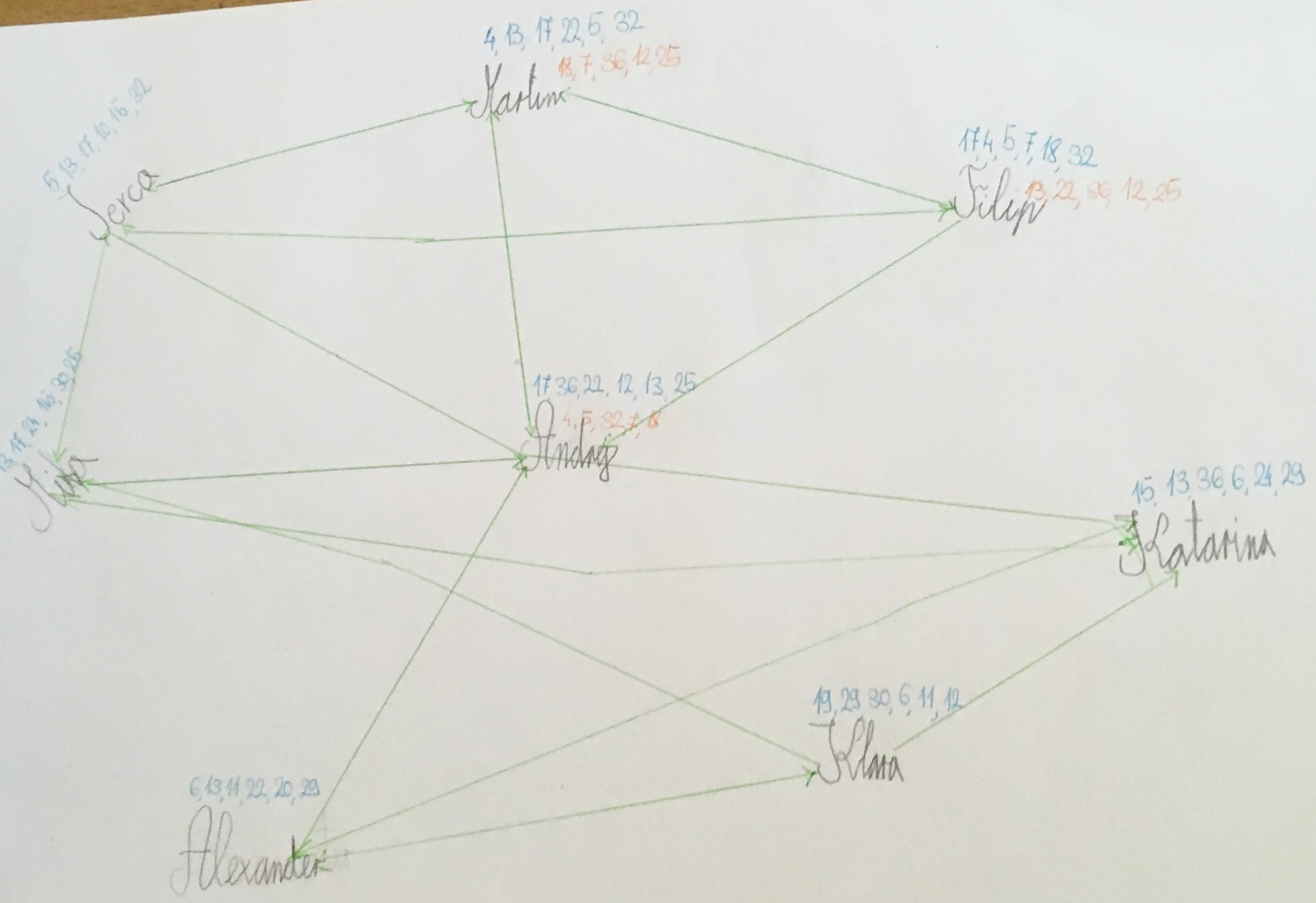
   Vsak član skupine k svojemu imenu z rdečo barvo pripiše številke risank, ki so jih izbrali tisti trije člani, ki so mu najbolj podobni. Če sta katere med njimi gledala dva od povezanih, te številke obkroži; če vsi trije, jih obkroži dvakrat.

   Te risanke so njegova priporočila: učenci lahko pogledajo, za katere risanke gre. Nekatere od njih že poznajo. So jim všeč? Priporočilni sistem deluje?

Priporočilni sistem v računalniku

Računalnik za učno uro ni potreben. Po izkušnjah je učencem tudi ta del sicer zanimiv, sami pa presodite, ali ga izvesti ali ne.

Priprava

Pred uro pripravimo pripravimo obrazec za vnos izborov. Izberemo temo (risanke, glasba ali lastna tema), število stvari, ki jih bodo morali učenci izbrati (privzeta nastavitev, 7, bi morala biti primerna) in dobimo povezavo, na primer https://data.pumice.si/princesa-zmaj. To povezavo vnesemo v tablice (ali računalnike), ki jih bodo učenci uporabljali za vnašanje podatkov.

Stran lahko tudi sami preskusite, tako da oddate nekaj izmišljenih izbir, ali pa poskusite primer izmišljenih podatkov. Za delo v razredu nato sestavite nov obrazec z novo povezavo.

Zbiranje podatkov

Ko so učenci dovolj daleč z delom (recimo med risanjem na papir A3), skupinam razdelimo tablice, v katere smo vnesli povezavo do obrazca. Učenci poiščejo in izberejo svoje risanke.

Analiza

Ko so podatki zbrani, lahko skupaj z učenci pogledamo rezultate za celoten razred. Ta del opravimo frontalno, na učiteljevem računalniku.

1. S programom Orange odprite že pripravljeni delotok. Takšen bo.

   

   Kaj pomenijo posamezne komponente, ni pomembno. Zadošča, da zamenjamo vir podatkov (glej spodaj) in opazujemo rezultate v končnih komponentah; vse ostalo naj bi delovalo samo. Kdor želi vedeti, kaj počne posamezen del delotoka, pa bo našel več v gradivo za učitelje.

2. 

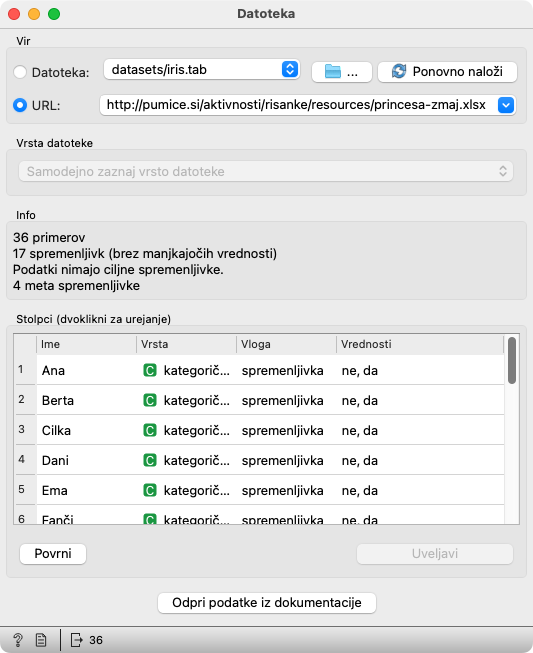
   Z dvoklikom odprite gradnik Datoteka in zamenjajte URL z URLjem za prenos podatkov, ki smo jih zbrali v razredu. Če je bil URL za zbiranje podatkov, ki smo ga vpisali v tablice, https://data.pumice.si/princesa-zmaj, bodo podatki na https://data.pumice.si/princesa-zmaj/data. Prepišite ga v polje URL in pritisnite Enter. V spodnjem delu se bodo izpisala imena vaših učencev. Slika kaže primer dekliškega razreda, v katerega prvih vrsticah sedijo Ana, Berta, Cilka, Dani, Ema in Fanči.

   Za vajo doma lahko delate s testnimi podatki s te strani. Povezava nanje, https://pumice.si/aktivnosti/risanke/resources/princesa-zmaj.xlsx, je že nastavljena v delotoku.

3. Nato z dvoklikom odprite Raziskovalec omrežja.

   

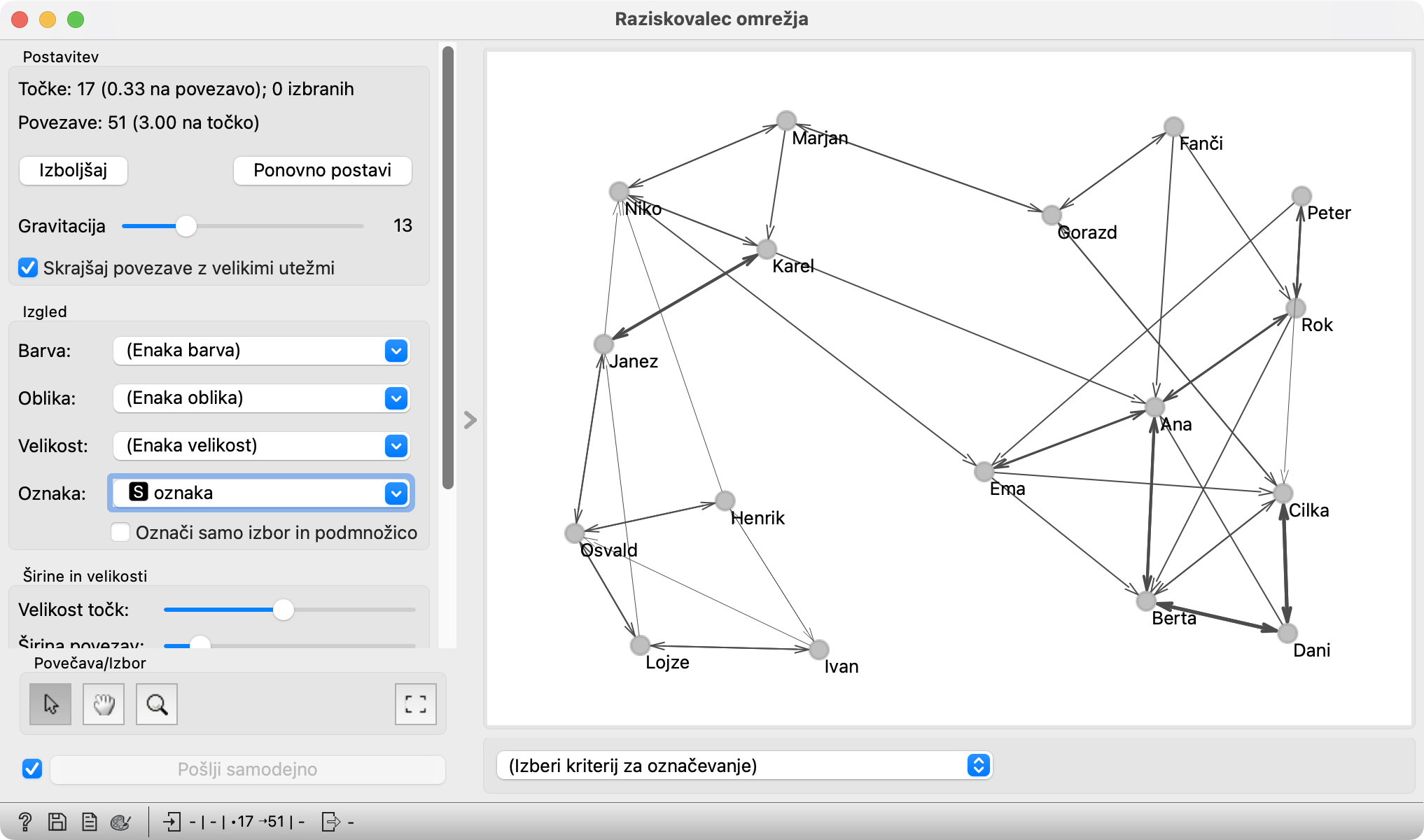
   Od vsakega učenca vodijo natančno tri puščice, ki kažejo na tiste tri, ki so učencu najbolj podobni. Slika bo drugačna od te, ki so jo narisale posamezne skupine, saj vsebuje podatke za ves razred.

   (Nasvet: če točke niso lepo razporejene, pritisnite Izboljšaj, če tudi to ne deluje, pa Ponovno postavi. Če je videti res grozno, zmanjšajte vrednost Gravitacija in jo nato ponovno povečajte.)

   Včasih dobimo v mreži izrazite skupine, ali pa se ločijo dečki od deklic. Vidimo tudi tiste, h katerih vodi več puščic - najbrž imajo bolj “osrednje” okuse - in tiste, h katerim ne vodi nobena puščica. Te lahko potolažimo, da je njihov okus poseben, torej “izbran”.

4. 

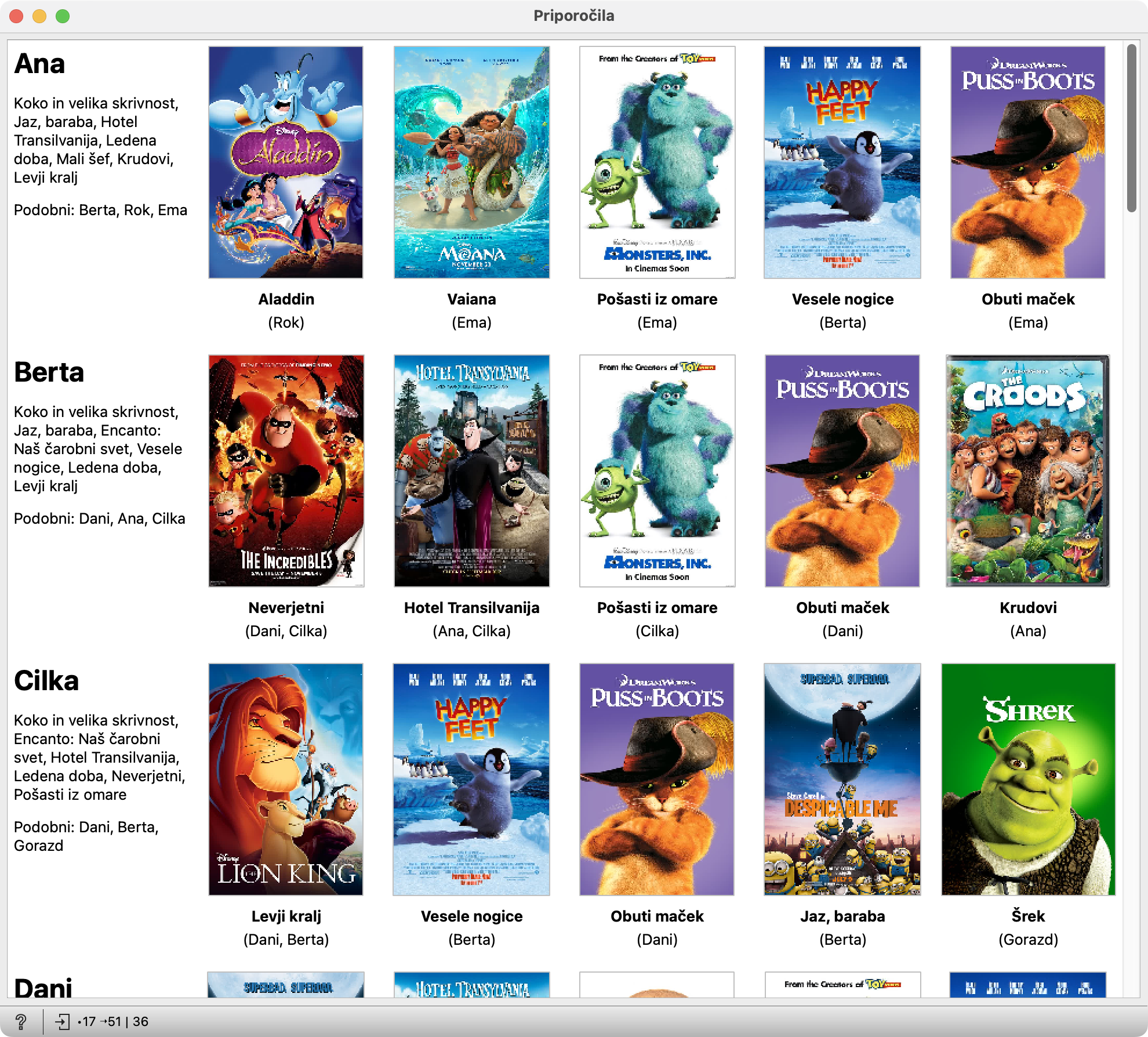
   Priporočila vidimo v gradniku Priporočila.

   Za vsakega učenca vidimo, katere risanke je izbral in kdo v razredu je izbiral podobne risanke. Predvsem pa vsakemu pokaže priporočila, pod priporočilom pa je napisano, kateri izmed njemu podobnih sošolcev in sošolk je za to priporočilo “zaslužen”.

Razširitve

Različne velikosti izborov

Če učencem dovolimo, da izbirajo različno število risank, podobnosti ne morejo računati kar kot število skupnih risank, saj bi si bili tisti, ki izberejo več risank, očitno podobnejši. Če se lotimo tako, je potrebno število skupnih risank deliti s številom vseh risank, ki jih je izbral eden ali drugi ali oba. Z bolj matematičnimi besedami: velikost preseka množic izbranih risank moramo deliti z velikostjo unije teh množic.

Za to je potrebno poznati decimalna števila, torej takšna aktivnost ne sodi ravno v četrti razred. Delno se je temu mogoče izogniti tako, da morajo število skupnih risank pomnožiti z deset ali celo 100 in nato izračunati celoštevilski količnik. Kakor presodite. :)

Drugačne teme

Ker starejših učencev - sploh pa dijakov - risanke praviloma ne zanimajo (oziroma tega mogoče ne smejo priznati), so zanje primernejša tema glasbeniki ali televizijske serije. Priporočamo slednje, saj so bolj zanimive ("A si že gledal to in to" je boljša iztočnica za klepet kot “A si že poslušal tega in tega”.)

Pripravimo lahko tudi svoje podatke z, na primer, izborom knjig. Detajli so opisani v dodatnem gradivu za učitelje.