Kaj počnejo palčki?

Ura predstavi delovanje preprostega algoritma strojnega učenja in modela. Pri starejših učencih jo lahko uporabimo kot pripravo na Prepoznavanje štirikotnikov; v tem primeru ne izpustimo opisa algoritma sestavljanja drevesa (glej Zaključek). Po želji lahko izpustimo del z računalnikom, vendar ne vzame veliko časa, pa tudi veliko učiteljevega znanja iz umetne inteligence ne zahteva.

Za mlajše je aktivnost morda zanimiva zato, ker zahteva prepoznavanje lastnosti in delitev objektov na podmnožice.

Prepoznavanje poklicev palčkov

V prvem delu ure učenci odkrijejo pravila, s katerimi prepoznajo poklice palčkov.

1. Razred razdelimo v skupine s po štirimi, petimi učenci.

2. 

   Razredu pokažemo sliki palčkov Lojzeta in Poldija: Lojza je rudar in Poldi je krojač. Nato jima pokažemo Slavka in Pepija. Vprašanje je: kaj sta Slavko in Pepi?

   To je seveda težko reči. Pa še huje je: palčki niso le rudarji in krojači temveč tudi vrtnarji in zidarji. Na srečo pa lahko posamezne poklice prepoznamo po izgledu palčkov.

3. 

   Otroke razdelimo v skupine. Vsaka skupina dobi komplet kartic. Za večino palčkov je na kartici napisan tudi poklic. Naloga učencev je ugotoviti, kakšno delo opravljajo Slavko, Božo, Emil, Pepi, Franci in Bojan. Njihove poklice napišejo na kartice.

   Najbrž bodo poskušali poiskati palčka, ki je popolnoma enak, recimo, Pepiju. Ni ga. Obstajajo pa pravila, skupne lastnosti, po katerih lahko prepoznamo, recimo, vrtnarje in jih ločimo od rudarjev.

4. Ko skupine določijo poklice teh šestih palčkov, jemljemo te palčke enega za drugim in sprašujemo skupine po njegovem poklicu. Načelno bi morale biti skupine soglasne. Če niso - pa tudi, če so - naj utemeljijo, zakaj so posameznega palčka uvrstile tako, kot so ga.

   Rezultate (imena in poklice palčkov, ali pa več poklicev, če nanese tako) zapišemo na tablo za morebitno kasnejšo rabo.

Odločitvena pravila in drevo

V naslednjem delu formalno zapišemo odkrita pravila.

1. Otroke vzpodbudimo, da povedo pravila za določanje poklicev. Pričakujemo nekaj takšnega:

   • če ima luč, je rudar;
   • če ima lopatko (vendar nima tudi luči!), je vrtnar;
   • če nima lopatke in ima zaponko na pasu, je krojač;
   • če nima ne lopatke ne zaponke, je zidar.

   Oblika pravil bo morda drugačna, poskrbite pa, da bodo na koncu oblikovali konkretna in točna pravila. Po presoji jih zapišite tablo. Skupaj lahko tudi pogledate, ali so njihova pravila nedvoumna in ali pravilno razvrstijo palčke, katerih poklic je znan.

   Pravila naj ne bi vsebovala barve čevljev, pasu in brade ter oblike ust in kape, saj so te lastnosti namerno razdeljene med palčke tako, da nam pri določanju poklica ne pomagajo.

2. Nato poskušamo pripeljati učence do ideje klasifikacijskega drevesa. To storimo tako, da vzamemo eno od slik, a jim je ne pokažemo. Določiti morajo poklic palčka na sliki. Če vprašajo po imenu, jim ga ne povemo. Pač pa lahko sprašujejo po lastnostih.

   Najverjetneje bodo začeli s svetilko ali lopato. Ko izvedo, ali jo palček ima, bodo vprašali po naslednji lastnosti in tako naprej, dokler ne izvedo poklica.

   Vajo ponovimo še z nekaj palčki. Za začetek lahko vzamemo rudarja, ki je najpreprostejši, nujno pa vključimo tudi zidarja in krojača.

3. Ko dovolj “utrdimo” spraševanje, da začutimo, da gre po dovolj ustaljeni poti, vprašamo učence, če bi znali pripraviti “recept” za določanje poklica? Torej nekakšna navodila za spraševanje?

   Najbrž bodo rekli, da najprej vprašamo ali ima svetilko ali pa ali ima lopato. Če začnejo z zaponko, jim to ne bo veliko pomagalo, saj bodo morali v vsakem primeru - ne glede na to, ali palček ima zaponko ali ne - zanj izvedeti še, ali ima svetilko ali lopato. Da je zaponka slab začetek, so se najbrž že naučili, ko so spraševali o konkretnih palčkih; če ne, jih na to spomnimo in ji pripravimo do tega, da začnejo s svetilko ali lopato - če je treba, jih omejimo, da morajo priti do odgovora z dvema vprašanjema.

   Njihovo prvo vprašanje kratko zapišemo (npr. “svetilka”). Potem morajo pokriti oba scenarija, torej, odgovor “ne” ali “da”. Od svetilke povlečemo črti levo in desno dol, nanju napišemo “ne” in “da”, pod črto pa naslednji vprašanji …

   Končni rezultat bo najbrž eno od spodnjih dveh dreves. Če namreč začnemo s svetilko ali lopato, to že določi, kakšne so smiselne naslednje delitve.

   

4. 

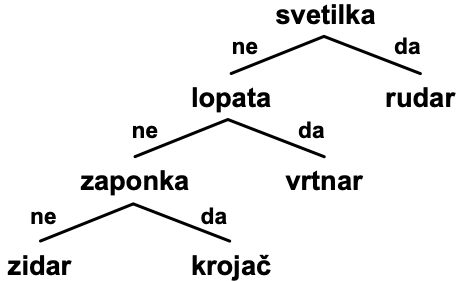
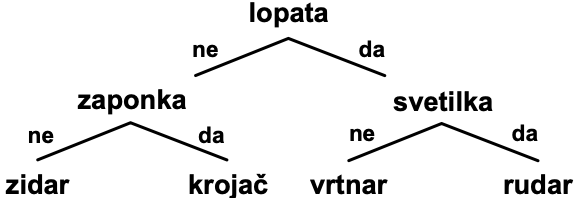
   Drevo, ki je narisano na tabli, določa ključ, s katerim lahko določimo poklic vsakemu novemu palčku, na katerega bi naleteli v gozdu. (Če ne bi bili v učilnici temveč v gozdu in če bi bili tam palčki.) To pokažemo tako, da vzamemo enega od palčkov (na primer eno od večjih slik) in mu določimo poklice tako, da ga postavimo na vrh drevesa in z njim “potujemo” po ustrezni poti do dna.

   Iz slik palčkov smo tako izluščili splošen vzorec, pravilo. Posamičnih slik zdaj sploh ne potrebujemo več, saj model (drevo) vsebuje vse, kar je potrebno.

Bi znal to tudi računalnik?

Kar smo naredili, je kar pametno: iz slik palčkov smo se naučili splošnega pravila. Bi znal to tudi računalnik? Ta del ure izvedemo frontalno.

1. Na računalniku odpremo Orange in naložimo pripravljeni delotok.

   

2. 

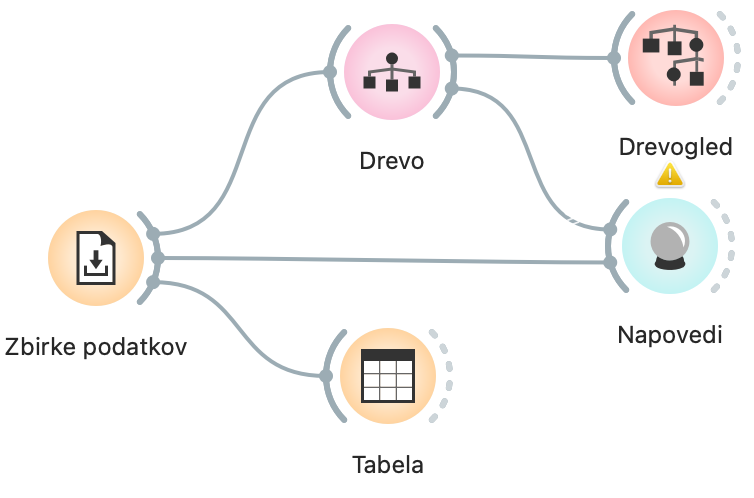
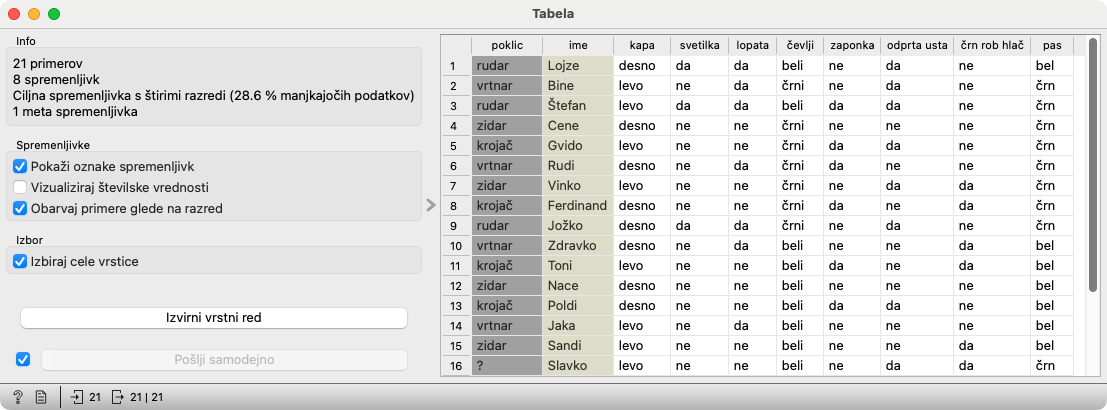
   Z dvoklikom odpremo gradnik Tabela, da učencem pokažemo podatke, s katerimi bo delal računalnik. To je pomembno zato, da vidijo, da vsebujejo tudi nepomembne lastnosti, kot so barva pasu, čevljev in oblika kape. Videli bomo, ali ga bodo zavedle ali ne.

3. Sestavljeno drevo vidimo v Drevogledu.

   

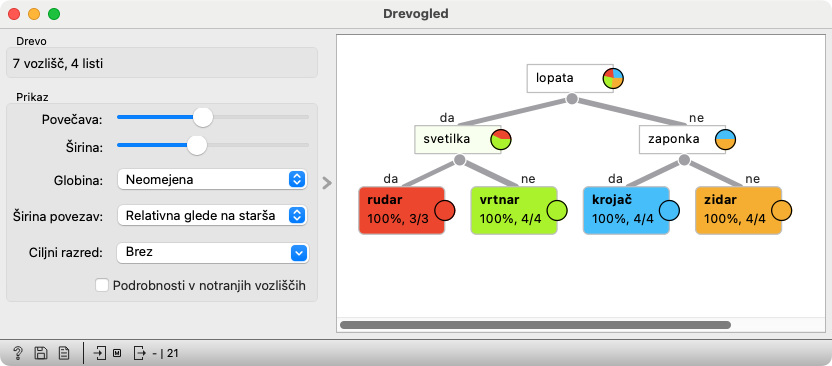
   Če so učenci dobili enako drevo, je to imenitno. Če so dobili drugo različico, je prav tako imenitno, saj lahko primerjamo obe drevesi in ugotovimo, da bosta, čeprav sta različni, napovedovali enake poklice.

4. 

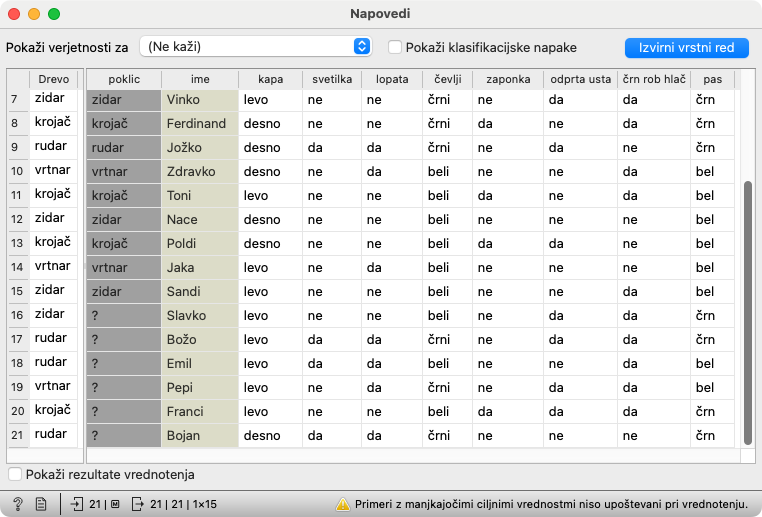
   V gradniku Napovedi vidimo, kakšne poklice je Palčkom napovedal računalnik. Pomaknemo se na konec tabele, pa vidimo poklice, ki jih računalnik napove za šesterico, katerih poklice so določali tudi učenci.

   So računalnikove napovedi enake napovedim učencev?

Zaključek

Učenci so se iz podatkov v obliki slik naučili določati poklice palčkov. Učenje zahteva pamet ali, z bolj učeno tujko, inteligence. Tudi računalnik se je učil, prav tako kot oni, torej je bil tudi on inteligenten. Ker ta inteligenca ni naravna, človeška, temveč umetna, ji rečemo umetna inteligenca. Področju umetne inteligence, ki se ukvarja s tem, kako se stroji (torej: računalniki) učijo, pa pravimo strojno učenje.

Ko se ljudje lotimo nekega opravila, navadno na sledimo receptom; pogosto kar nekako “vemo”, kako se lotiti dela. Da računalnik kaj naredi, pa ga moramo sprogramirati. Tudi umetna inteligenca je samo program, s katerim računalnik sledi navodilom, ki si jih je zamislil programer.

Da se je torej računalnik naučil razlikovanja med palčki, je moral programer sestaviti program, postopek, recept za sestavljanje drevesa. Ta je preprost: med vsemi možnimi lastnostmi poišče tisto, ki “dobro razdeli palčke”. Računalnik je opazil, da podatek o tem, ali ima palček lopato, razdeli palčke na vrtnarje in rudarje na eni ter zidarje in krojače na drugi strani. Ko je, po drugi strani, preveril podatek o barvi pasu, je videl, da so tako med tistimi z belim in črnim pasom palčki različnih poklicev. Ker je dobil podatek o lopati najvišjo oceno, je palčke razdelil glede na to lastnost v dve skupini. Nato je v vsaki od podskupin ponovno ocenil vse lastnosti. Ker ga je to pripeljalo do podskupin, v katerih imajo vsi palčki isti poklic, je bilo delo končano.

Če aktivnost služi kot uvod v druge aktivnosti, ki zahtevajo razumevanje sestavljanja drevesa, je najboljše, da algoritem pokažemo še “fizično”, tako da opazujemo in delimo listke s palčki v podskupine.

Postopek, ki smo ga spoznali, ni uporaben le za palčke. Kaj, če bi si zapisovali simptome bolezni (vročina, kašelj, slabost, glavobol, boleče grlo, poln nos, boleč želodec) in za katero bolezen je šlo (prehlad, gripa, viroza)? Če bi takšne podatke pokazali računalniku, bi nam ta lahko povedal, katero bolezen imamo. Lahko bi zapisovali lastnosti šolskih malic (je sladka? ima mleko? je zraven kruh?) in ali je bila tisti dan malica neki sošolki Petri všeč ali ne. Morda bi znal računalnik povedati, kako se Petra odloča, ali ji bo malica všeč ali ne in ali jo bo všeč kruh z marmelado, ki bo na jedilniku jutri.

Takšni postopki so se v resnici uporabljali, na primer v medicini. Z njimi smo poskušali napovedovati uspešnost operacij, določati bolezni, učinkovitost zdravil … Tudi danes uporabljamo podobne modele, le da zmorejo še veliko več, zato pa so tudi veliko bolj zapleteni ter potrebujejo več podatkov in boljše računalnike.